贪心算法解题套路框架

举个简单的例子，就能直观的展现贪心算法了。

比方说现在有两种钞票，面额分为为 1 元和 100 元，每种钞票的数量无限，但现在你只能选择 10 张，请问你应该如何选择，才能使得总金额最大？

那你肯定会说，这还用问么？肯定是 10 张全拿 100 元的钞票，共计 1000 元，这就是最优策略，但凡犹豫一秒就是傻瓜。

你这么说，也对，也不对。

说你对，因为这确实是最优解法，没毛病。

说你不对，是因为这个解法暴露的是你只想捞钱的本质 (¬‿¬) ，跳过了算法的产生、优化过程，不符合计算机思维。

那计算机就要提问了，一切算法的本质是穷举，现在你还没有穷举出所有可能的解法，凭什么说这就是最优解呢？

按照算法思维，这个问题的本质是做 10 次选择，每次选择有两种可能，分别是 1 元和 100 元，一共有 2（指数 10）种可能的选择。

所以你心里首先应该出现一棵高度为 10 的二叉树来穷举所有可行解，遍历这些可行解，然后可以得到最优解。

心里只要有这样一棵二叉树，就应该能写出代码：


// 定义：做 n 次选择，返回可以获得的最大金额
int findMax(int n) {
    if (n == 0) return 0;

    // 这次选择 1 元，然后递归求解剩下的 n - 1 次选择的最大值
    int result1 = 1 + findMax(n - 1);
    // 这次选择 100 元，然后递归求解剩下的 n - 1 次选择的最大值
    int result2 = 100 + findMax(n - 1);

    // 返回两种选择中的最大值
    return Math.max(result1, result2);
}

这个算法的复杂度是二叉树的节点数量，是指数级别，非常高。不过到这里你应该已经看出来了，findMax(n - 1) 的值肯定都一样，那么 100 + findMax(n - 1) 必然大于 1 + findMax(n - 1)，因此可以进行优化：

// 优化一、没必要对两种选择进行比较了
int findMax(int n) {
    if (n == 0) return 0;
    int result = 100 + findMax(n - 1);
    return result;
}

// 优化二、递归改为迭代
int findMax(int n) {
    int result = 0;
    for (int i = 0; i < n; i++) {
        result += 100;
    }
    return result;
}

// 优化三、直接计算结果就行了
int findMax(int n) {
    return 100 * n;
}

这就是贪心算法，复杂度从 O(2 指数 n) 优化到了 O(1)，堪称离谱。

你可能会认为这个例子太简单？

其实算法本来就很简单，就是穷举，有什么了不起的嘛？围绕穷举，衍生出各种优化方法，起了些花里胡哨的名字，不懂的人就容易被名字骗到，其实从原理上讲，没多大差别，不过是见招拆招罢了。

上面的例子虽然简单，但已经蕴含了贪心算法的精髓。接下来我们拓展延伸一下，在真实的算法问题中，如何发现贪心选择性质，如何用贪心算法解决问题。

贪心选择性质

首先来举例说明什么是贪心选择性质。

本文开头举例的这个最大金额的问题符合贪心选择性质，所以我们可以用贪心算法，把 O(2 指数 n) 的暴力穷举算法直接优化到了 O(1)。

作为对比，我们稍微改一改题目：

现在有两种钞票，面额分别为 1 元和 100 元，每种钞票的数量无限。现在给你一个目标金额 amount，请问你最少需要多少张钞票才能凑出这个金额？

这道题其实就是动态规划解题套路框架中讲解的凑零钱问题。

为了方便讲解，本文开头的最大金额问题我们称为「问题一」，这里的最少钞票数量问题我们称为「问题二」。

我们是如何解决问题二的？首先也是抽象出递归树，写出指数级别的暴力穷举算法，然后发现了重叠子问题，于是用备忘录消除重叠子问题，这就是标准的动态规划算法的求解过程，不能再优化了。

所以，问题二和问题一到底有什么区别？区别在于，前者没有贪心选择性质，而后者有。

贪心选择性质

贪心选择性质就是说能够通过局部最优解直接推导出全局最优解。

结合案例来说，对于问题一，局部最优解就是每次都选择 100 元，因为 100 > 1；对于问题二，局部最优解也是每次都选择 100 元，因为每张面额尽可能大，所需的钞票数量就能尽可能少。

但区别在于，问题一中每一次选择的局部最优解组合起来就是全局最优解，而问题二中不是。

比方说目标金额 amount = 3，虽然每次选择 100 元是局部最优解，但想凑出 3 元，只能选择 3 张 1 元，局部最优解不一定能构成全局最优解。

对于问题二的场景，不符合贪心选择性质，所以不能用贪心算法，只能穷举所有可行解，才能计算出最优解。

贪心选择性质 vs 最优子结构

动态规划解题套路框架 中提到，算法问题必须要有「最优子结构」性质，才能通过子问题的最优解推导出全局最优解，这是动态规划算法的基础。

那么就有读者搞不清楚了，这个「贪心选择性质」和「最优子结构」有什么区别？

最优子结构的意思是说，现在我已经把所有子问题的最优解都求出来了，然后我可以基于这些子问题的最优解推导出原问题的最优解。

贪心选择性质的意思是说，我只需要进行一些局部最优的选择策略，就能直接知道哪个子问题的解是最优的了，且这个局部最优解可以推导出原问题的最优解。此时此刻我就能知道，不需要等到所有子问题的解算出来才知道。

所以贪心算法的效率一般都比较高，因为它不需要遍历完整的解空间。

例题实战

先来看第一道例题，力扣第 55 题「跳跃游戏」：

注意题目说 nums[i] 表示可以跳跃的最大长度，不是固定长度。假设 nums[i] = 3，意味着你可以在索引 i 往前跳 1 步、2 步或 3 步。

我们先思考暴力穷举解法吧，如何穷举所有可能的跳跃路径？你心里的那棵多叉树画出来了没有？

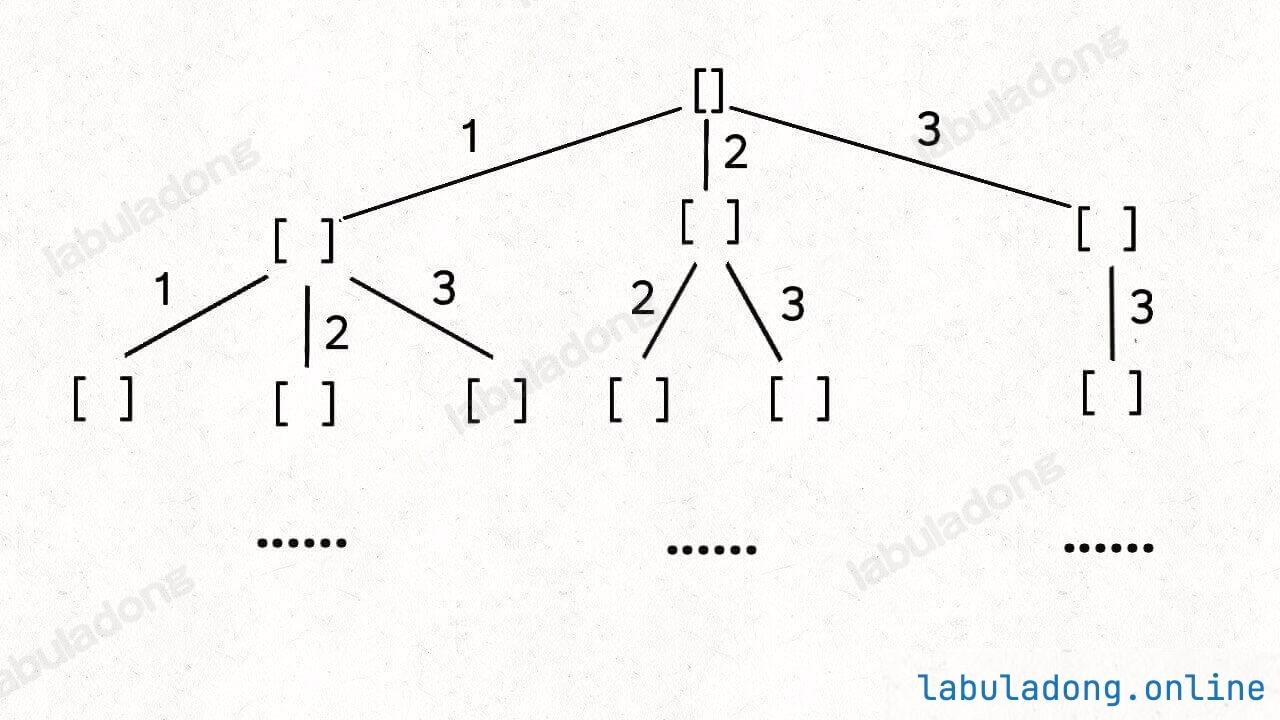
假设 N 为 nums 的长度，这道题相当于做 N 次选择，每次选择有 nums[i] 种选项，想要穷举所有的跳跃路径，就是一棵高度为 N 的多叉树，每个节点有 nums[i] 个子节点：

这个算法本质上还是穷举了所有可能的选择，可以走动态规划那一套流程进行优化，但是这里我们先不急，可以再仔细想想，这个问题有没有贪心选择性质？

题目的关键点：

1、在索引 i，可以跳跃 1 ~ nums[i] 步。

2、只要能跳到最后一个索引，就返回 true。

这里面有个细节，比方说你现在站在 nums[i] = 3 的位置，你可以跳到 i+1, i+2, i+3 三个位置，此时你真的需要分别跳过去，然后递归求解子问题 dp(i+1), dp(i+2), dp(i+3)，最后通过子问题的答案来决定 dp(i) 的结果吗？

其实不用的，i+1, i+2, i+3 三个候选项，它们谁能走得最远，你就选谁，准没错。

具体来说，i+1 能走到的最远距离是 i+1+nums[i+1]，i+2 能走到的最远距离是 i+2+nums[i+2]，i+3 能走到的最远距离是 i+3+nums[i+3]，你看看谁最大，就选谁。

这就是贪心选择性质，通过局部最优解就能推导全局最优解，不需要等到递归计算出所有子问题的答案才能做选择。

所以这道题的最优解法如下：

func canJump(nums []int) bool {
    n := len(nums)
    farthest := 0
    for i := 0; i < n-1; i++ {
        // 不断计算能跳到的最远距离
        farthest = max(farthest, i+nums[i])
        // 可能碰到了 0，卡住跳不动了
        if farthest <= i {
            return false
        }
    }
    return farthest >= n-1
}

// Helper function to return the max of two integers
func max(a, b int) int {
    if a > b {
        return a
    }
    return b
}

只需要遍历所有元素，记录当前能到达的最远位置就行了，时间复杂度是 O(N)，空间复杂度是 O(1)，非常高效。

接下来看第二道例题，力扣第 45 题「跳跃游戏 II」：

现在的问题是，保证你一定可以跳到最后一格，请问你最少要跳多少次，才能跳过去。

暴力穷举肯定也是可以做的，就类似上面的那道题，只不过修改一下 dp 数组的定义，返回值从 boolean 改成 int，表示最少需要跳跃的次数就行了。

题目问的就是 dp(nums, 0) 的结果，base case 就是当 p 超过最后一格时，不需要跳跃：

if (p >= nums.length - 1) {
    return 0;
}

根据前文动态规划套路详解的动规框架，就可以暴力穷举所有可能的跳法，通过备忘录 memo 消除重叠子问题，取其中的最小值最为最终答案：

func jump(nums []int) int {
    n := len(nums)
    // 备忘录都初始化为 n，相当于 INT_MAX
    // 因为从 0 跳到 n - 1 最多 n - 1 步
    memo := make([]int, n)
    for i := range memo {
        memo[i] = n
    }

    return dp(nums, 0, memo)
}

// 定义：从索引 p 跳到最后一格，至少需要 dp(nums, p) 步
func dp(nums []int, p int, memo []int) int {
    n := len(nums)
    // base case
    if p >= n - 1 {
        return 0
    }
    // 子问题已经计算过
    if memo[p] != n {
        return memo[p]
    }
    steps := nums[p]
    // 你可以选择跳 1 步，2 步...
    for i := 1; i <= steps; i++ {
        // 穷举每一个选择
        // 计算每一个子问题的结果
        subProblem := dp(nums, p+i, memo)
        // 取其中最小的作为最终结果
        memo[p] = min(memo[p], subProblem+1)
    }
    return memo[p]
}

这个解法已经通过备忘录消除了冗余计算，时间复杂度是递归深度 x 每次递归需要的时间复杂度，即 O(N²)，在 LeetCode 上是无法通过所有用例的，会超时。

所以进一步的优化就只能是贪心算法了，我们要仔细思考是否存在贪心选择性质，是否能够通过局部最优解推导全局最优解，避免全量穷举所有的可能解。

和上面的题目是一样的优化思路：我们真的需要递归地计算出每一个子问题的结果，然后求最值吗？其实不需要。

hexinkuangjia67

上图这种情况，我们站在索引 0 的位置，可以向前跳 1，2 或 3 步，你说应该选择跳多少呢？

你可以确定地说，应该跳 2 步调到索引 2，因为 nums[2] 的可跳跃区域涵盖了索引区间 [3..6]，比其他的都大。题目求最少的跳跃次数，那么往索引 2 跳必然是最优的选择。

这就是贪心选择性质，我们不需要真的递归穷举出所有选择的具体结果来比较求最值，而只需要每次选择那个最有潜力的局部最优解，最终就能得到全局最优解。

绕过这个弯儿来就可以写代码了。代码可能有点不好理解，关键在于对 i, end, farthest, jumps 几个变量的更新：

每次跳跃可达的是一个索引区间，代码中 [i, end] 维护当前的跳跃次数 jumps 可以覆盖的索引区间，farthest 表示从 [i, end] 区间内起跳，可以跳到的最远索引。

可以结合代码注释和可视化来理解：

func jump(nums []int) int {
    if len(nums) <= 1 {
        return 0
    }
    n := len(nums)
    // jumps 步可以跳到索引区间 [i, end]
    end, jumps := 0, 0
    // 在 [i, end] 区间内，最远可以跳到的索引是 farthest
    farthest := 0
    for i := 0; i < n-1; i++ {
        // 计算从索引 i 可以跳到的最远索引
        if nums[i]+i > farthest {
            farthest = nums[i] + i
        }
        if i == end {
            // [i, end] 区间是 jumps 步可达的索引范围
            // 现在已经遍历完 [i, end]，所以需要再跳一步
            jumps++
            end = farthest
            if farthest >= n-1 {
                // 如果已经可以到达终点，则可以直接返回
                return jumps
            }
        }
    }
    // 如果无法到达终点，则返回 -1
    return -1
}

这个解法的时间复杂度是 O(N)，空间复杂度是 O(1)，可以通过所有测试用例。

至此，两道例题都解决了。

贪心算法的解题步骤

贪心算法的关键在于问题是否具备贪心选择性质，所以只能具体问题具体分析，没办法抽象出一套固定的算法模板或者思维模式，判断一道题是否是贪心算法。

我的经验是，没必要刻意地识别一道题是否具备贪心选择性质。你只需时刻记住，算法的本质是穷举，遇到任何题目都要先想暴力穷举思路，穷举的过程中如果存在冗余计算，就用备忘录优化掉。

如果提交结果还是超时，那就说明不需要穷举所有的解空间就能求出最优解，这种情况下肯定需要用到贪心算法。你可以仔细观察题目，是否可以提前排除掉一些不合理的选择，是否可以直接通过局部最优解推导全局最优解。