回溯算法秒杀所有排列/组合/子集问题
虽然排列、组合、子集系列问题是高中就学过的,但如果想编写算法解决它们,还是非常考验计算机思维的,本文就讲讲编程解决这几个问题的核心思路,以后再有什么变体,你也能手到擒来,以不变应万变。
无论是排列、组合还是子集问题,简单说无非就是让你从序列 nums 中以给定规则取若干元素,主要有以下几种变体:
形式一、元素无重不可复选,即 nums 中的元素都是唯一的,每个元素最多只能被使用一次,这也是最基本的形式。
以组合为例,如果输入 nums = [2,3,6,7],和为 7 的组合应该只有 [7]。
形式二、元素可重不可复选,即 nums 中的元素可以存在重复,每个元素最多只能被使用一次。
以组合为例,如果输入 nums = [2,5,2,1,2],和为 7 的组合应该有两种 [2,2,2,1] 和 [5,2]。
形式三、元素无重可复选,即 nums 中的元素都是唯一的,每个元素可以被使用若干次。
以组合为例,如果输入 nums = [2,3,6,7],和为 7 的组合应该有两种 [2,2,3] 和 [7]。
当然,也可以说有第四种形式,即元素可重可复选。但既然元素可复选,那又何必存在重复元素呢?元素去重之后就等同于形式三,所以这种情况不用考虑。
上面用组合问题举的例子,但排列、组合、子集问题都可以有这三种基本形式,所以共有 9 种变化。
除此之外,题目也可以再添加各种限制条件,比如让你求和为 target 且元素个数为 k 的组合,那这么一来又可以衍生出一堆变体,怪不得面试笔试中经常考到排列组合这种基本题型。
但无论形式怎么变化,其本质就是穷举所有解,而这些解呈现树形结构,所以合理使用回溯算法框架,稍改代码框架即可把这些问题一网打尽。
具体来说,你需要先阅读并理解前文 回溯算法核心套路,然后记住如下子集问题和排列问题的回溯树,就可以解决所有排列组合子集相关的问题:
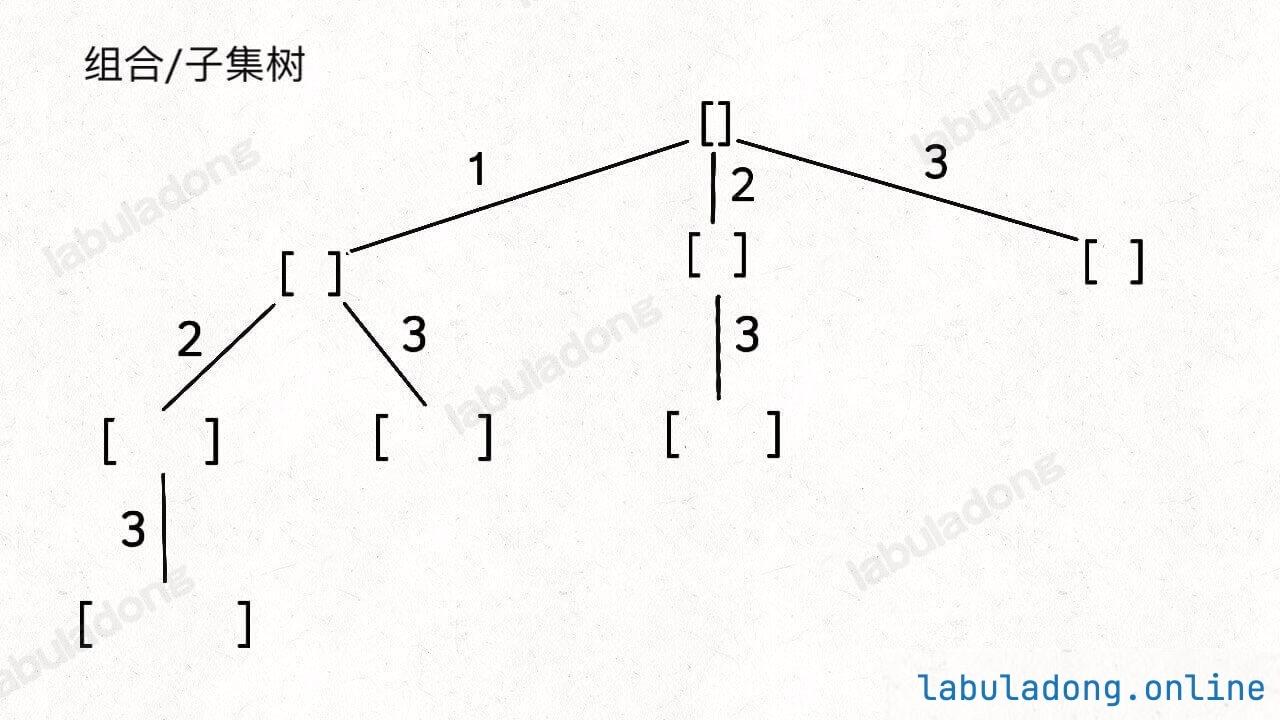
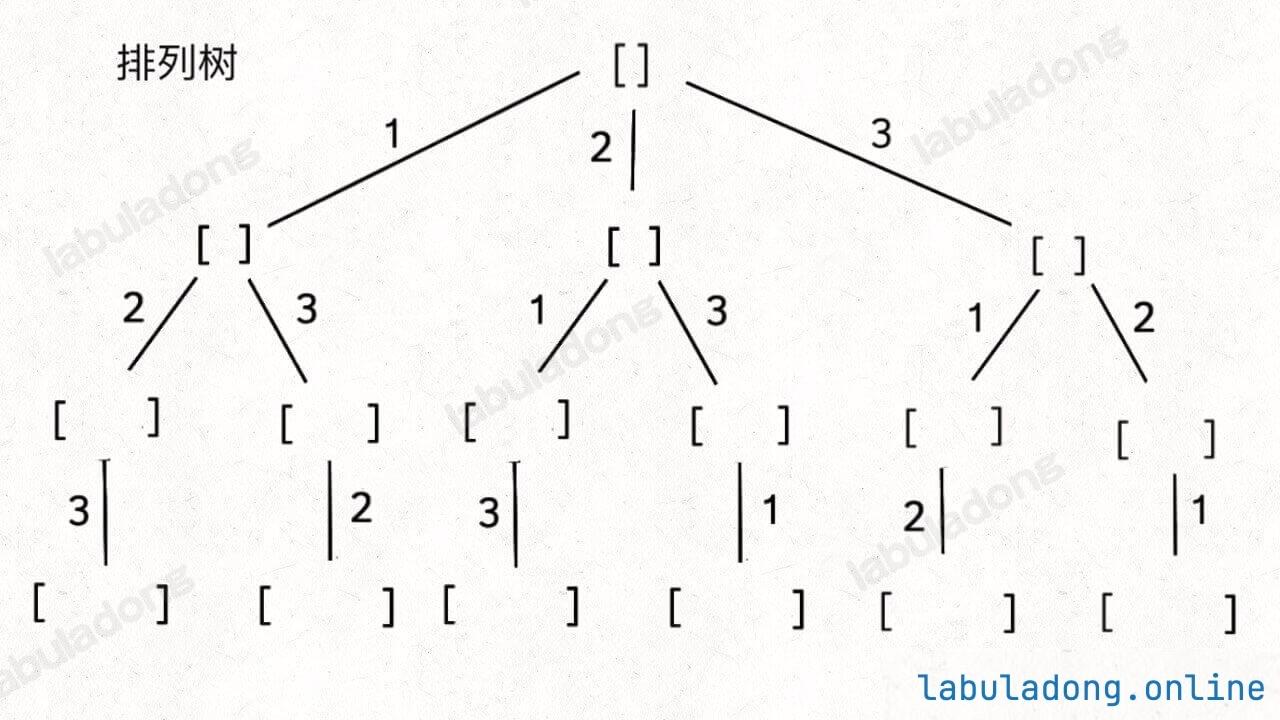
为什么只要记住这两种树形结构就能解决所有相关问题呢?
首先,组合问题和子集问题其实是等价的,这个后面会讲;至于之前说的三种变化形式,无非是在这两棵树上剪掉或者增加一些树枝罢了。
那么,接下来我们就开始穷举,把排列/组合/子集问题的 9 种形式都过一遍,学学如何用回溯算法把它们一套带走。
子集(元素无重不可复选)
力扣第 78 题「子集」就是这个问题:
题目给你输入一个无重复元素的数组 nums,其中每个元素最多使用一次,请你返回 nums 的所有子集。
比如输入 nums = [1,2,3],算法应该返回如下子集:
[ [],[1],[2],[3],[1,2],[1,3],[2,3],[1,2,3] ]
好,我们暂时不考虑如何用代码实现,先回忆一下我们的高中知识,如何手推所有子集?
首先,生成元素个数为 0 的子集,即空集 [],为了方便表示,我称之为 S_0。
然后,在 S_0 的基础上生成元素个数为 1 的所有子集,我称为 S_1:
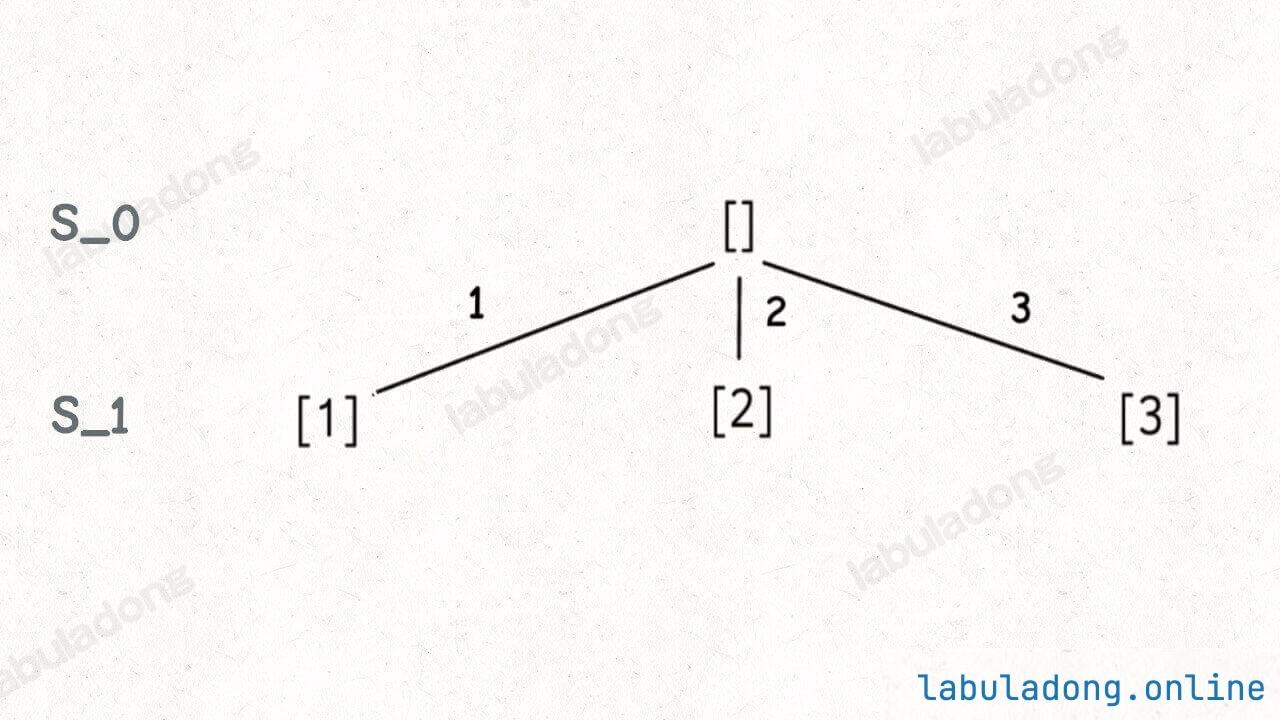
接下来,我们可以在 S_1 的基础上推导出 S_2,即元素个数为 2 的所有子集:
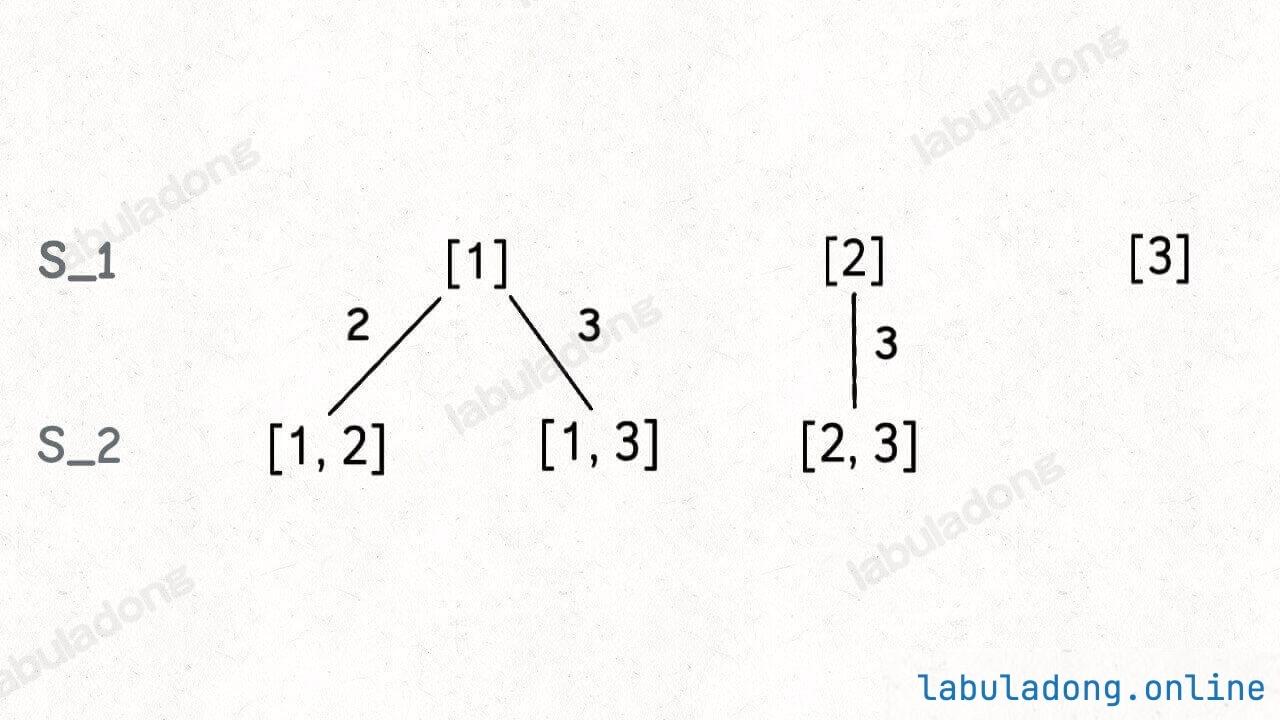
为什么集合 [2] 只需要添加 3,而不添加前面的 1 呢?
因为集合中的元素不用考虑顺序,[1,2,3] 中 2 后面只有 3,如果你添加了前面的 1,那么 [2,1] 会和之前已经生成的子集 [1,2] 重复。
换句话说,我们通过保证元素之间的相对顺序不变来防止出现重复的子集。
接着,我们可以通过 S_2 推出 S_3,实际上 S_3 中只有一个集合 [1,2,3],它是通过 [1,2] 推出的。
整个推导过程就是这样一棵树:
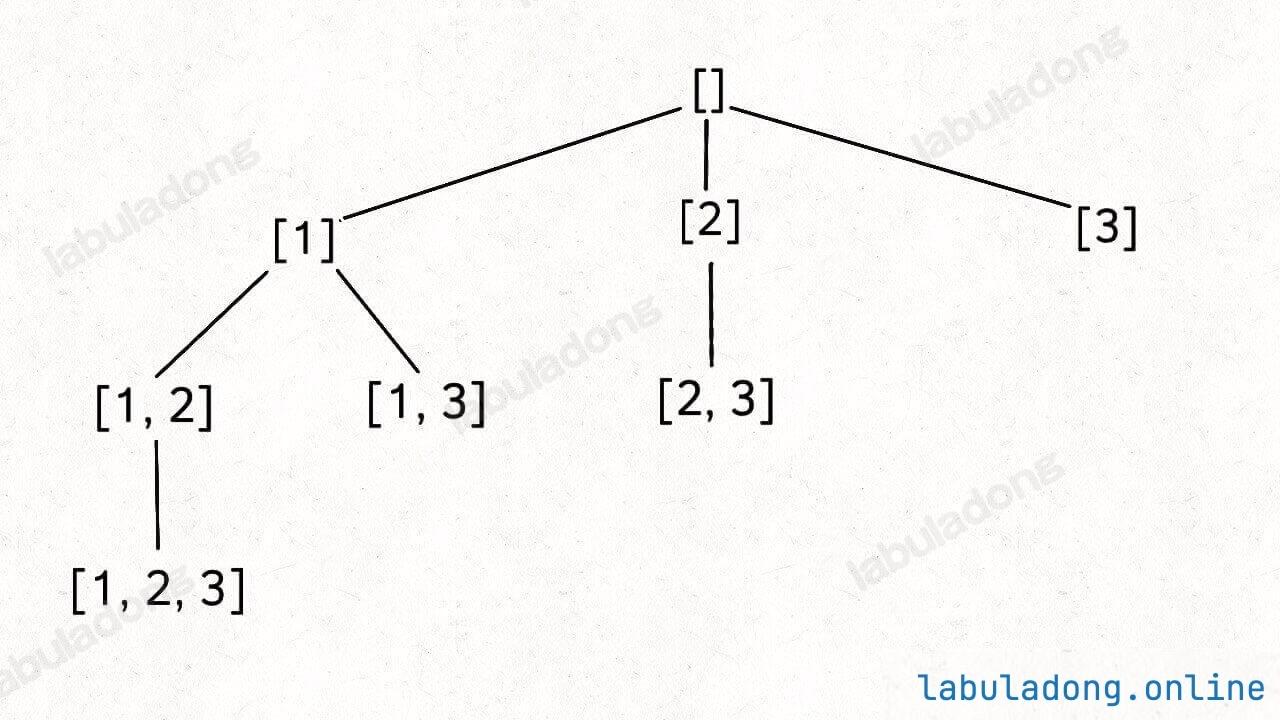
注意这棵树的特性:
如果把根节点作为第 0 层,将每个节点和根节点之间树枝上的元素作为该节点的值,那么第 n 层的所有节点就是大小为 n 的所有子集。
你比如大小为 2 的子集就是这一层节点的值:
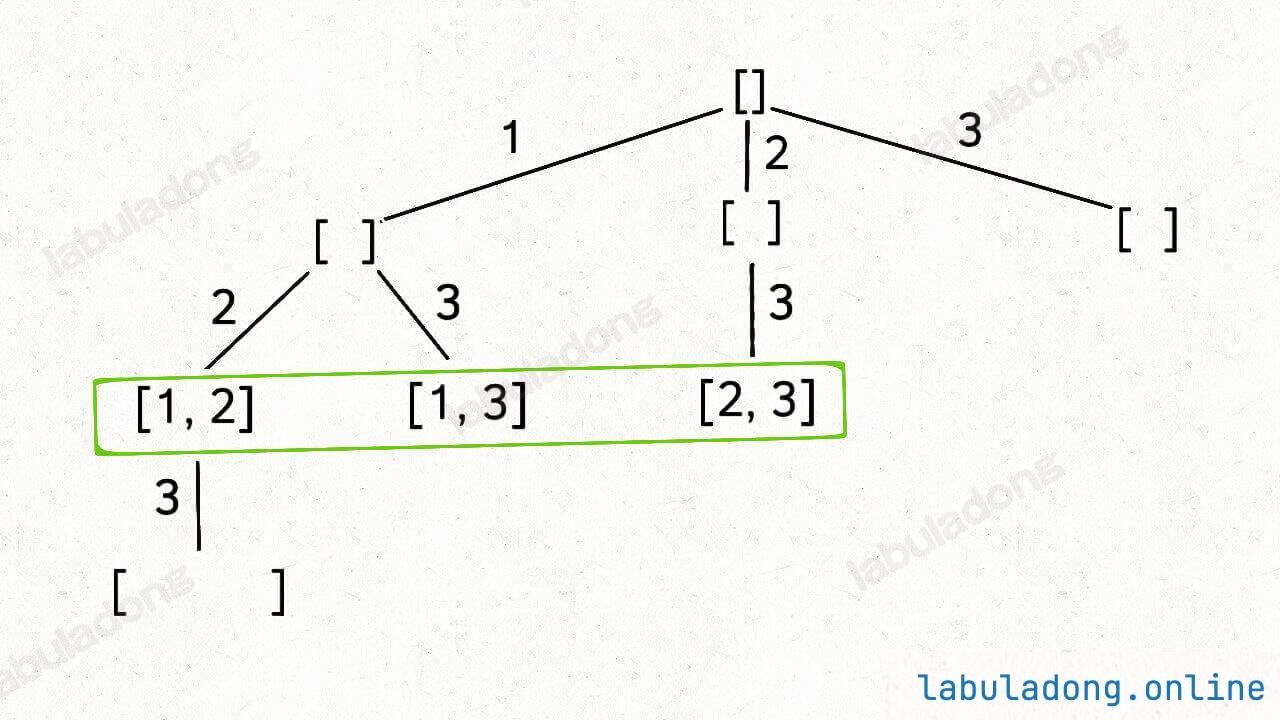
注意,本文之后所说「节点的值」都是指节点和根节点之间树枝上的元素,且将根节点认为是第 0 层。
那么再进一步,如果想计算所有子集,那只要遍历这棵多叉树,把所有节点的值收集起来不就行了?
直接看代码:
func subsets(nums []int) [][]int {
var res [][]int
// 记录回溯算法的递归路径
var track []int
// 回溯算法核心函数,遍历子集问题的回溯树
var backtrack func(int)
backtrack = func(start int) {
// 前序位置,每个节点的值都是一个子集
res = append(res, append([]int(nil), track...))
// 回溯算法标准框架
for i := start; i < len(nums); i++ {
// 做选择
track = append(track, nums[i])
// 通过 start 参数控制树枝的遍历,避免产生重复的子集
backtrack(i + 1)
// 撤销选择
track = track[:len(track)-1]
}
}
backtrack(0)
return res
}
看过前文 回溯算法核心框架 的读者应该很容易理解这段代码吧,我们使用 start 参数控制树枝的生长避免产生重复的子集,用 track 记录根节点到每个节点的路径的值,同时在前序位置把每个节点的路径值收集起来,完成回溯树的遍历就收集了所有子集:
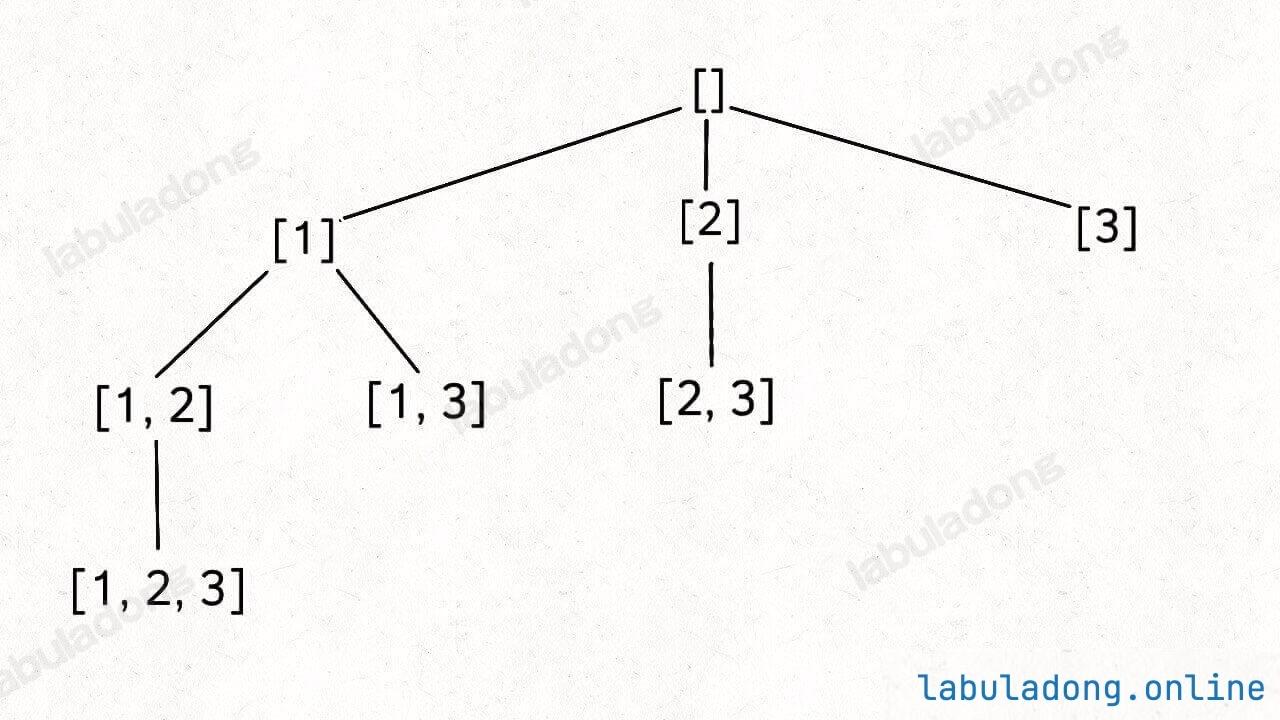
最后,backtrack 函数开头看似没有 base case,会不会进入无限递归?
其实不会的,当 start == nums.length 时,叶子节点的值会被装入 res,但 for 循环不会执行,也就结束了递归。
组合(元素无重不可复选)
如果你能够成功的生成所有无重子集,那么你稍微改改代码就能生成所有无重组合了。
你比如说,让你在 nums = [1,2,3] 中拿 2 个元素形成所有的组合,你怎么做?
稍微想想就会发现,大小为 2 的所有组合,不就是所有大小为 2 的子集嘛。
所以我说组合和子集是一样的:大小为 k 的组合就是大小为 k 的子集。
比如力扣第 77 题「组合」:
给定两个整数 n 和 k,返回范围 [1, n] 中所有可能的 k 个数的组合。
比如 combine(3, 2) 的返回值应该是:
[ [1,2],[1,3],[2,3] ]
这是标准的组合问题,但我给你翻译一下就变成子集问题了:
给你输入一个数组 nums = [1,2..,n] 和一个正整数 k,请你生成所有大小为 k 的子集。
还是以 nums = [1,2,3] 为例,刚才让你求所有子集,就是把所有节点的值都收集起来;现在你只需要把第 2 层(根节点视为第 0 层)的节点收集起来,就是大小为 2 的所有组合:
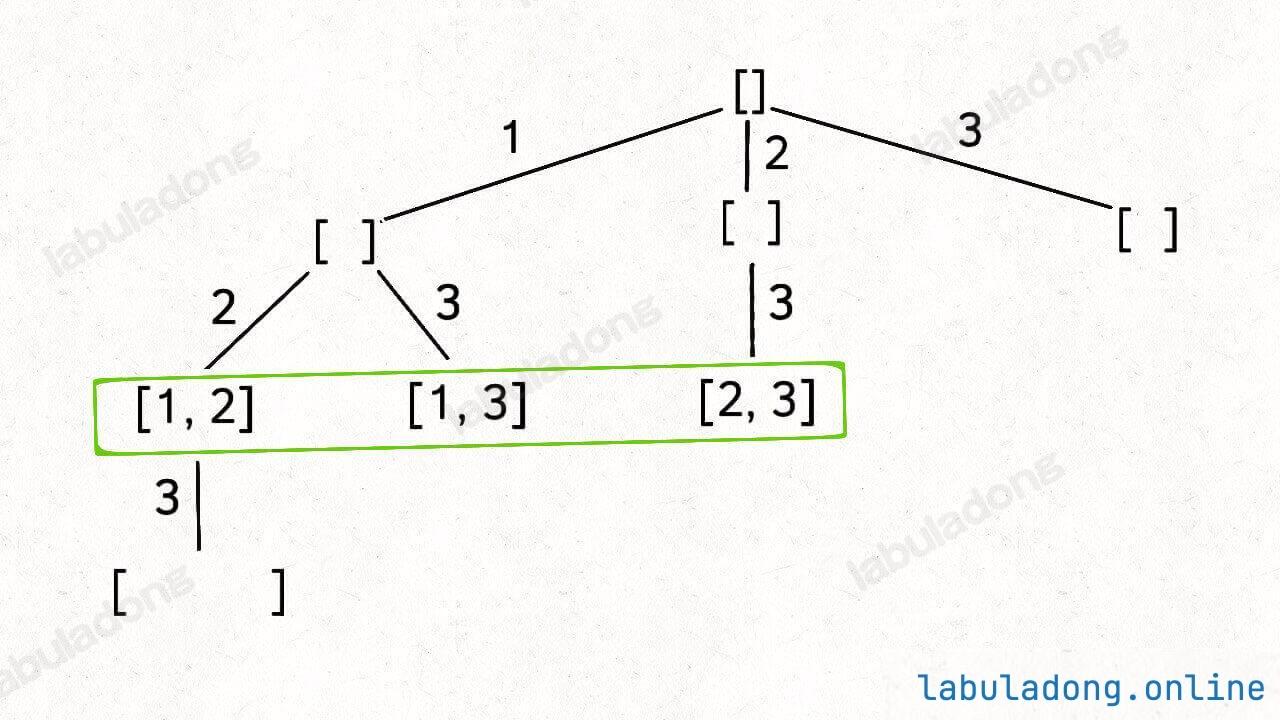
反映到代码上,只需要稍改 base case,控制算法仅仅收集第 k 层节点的值即可:
func combine(n int, k int) [][]int {
var res [][]int
// 记录回溯算法的递归路径
var track []int
// 回溯算法核心函数
var backtrack func(int)
backtrack = func(start int) {
// base case
if k == len(track) {
// 遍历到了第 k 层,收集当前节点的值
res = append(res, append([]int(nil), track...))
return
}
// 回溯算法标准框架
for i := start; i <= n; i++ {
// 选择
track = append(track, i)
// 通过 start 参数控制树枝的遍历,避免产生重复的子集
backtrack(i + 1)
// 撤销选择
track = track[:len(track)-1]
}
}
backtrack(1)
return res
}
这样,标准的组合问题也解决了。
排列(元素无重不可复选)
排列问题在前文 回溯算法核心框架 讲过,这里就简单过一下。
力扣第 46 题「全排列」就是标准的排列问题:
给定一个不含重复数字的数组 nums,返回其所有可能的全排列。
比如输入 nums = [1,2,3],函数的返回值应该是:
[
[1,2,3],[1,3,2],
[2,1,3],[2,3,1],
[3,1,2],[3,2,1]
]
刚才讲的组合/子集问题使用 start 变量保证元素 nums[start] 之后只会出现 nums[start+1..] 中的元素,通过固定元素的相对位置保证不出现重复的子集。
但排列问题本身就是让你穷举元素的位置,nums[i] 之后也可以出现 nums[i] 左边的元素,所以之前的那一套玩不转了,需要额外使用 used 数组来标记哪些元素还可以被选择。
标准全排列可以抽象成如下这棵多叉树:
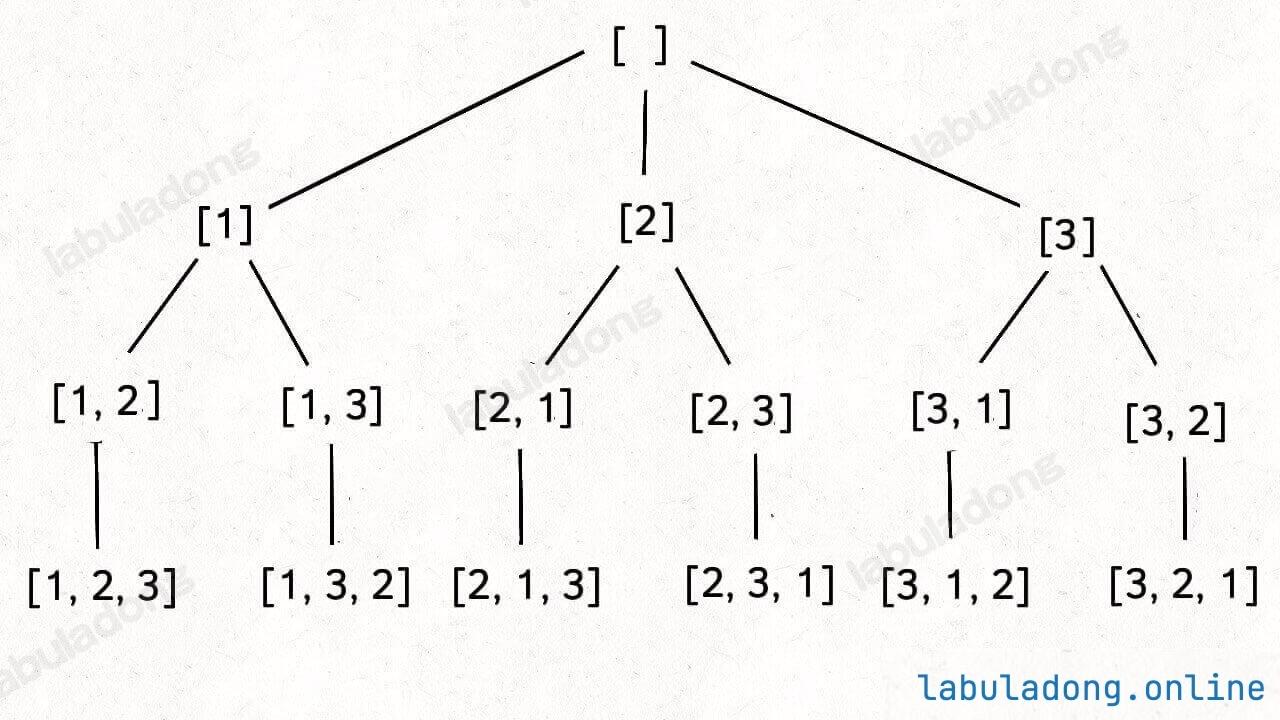
我们用 used 数组标记已经在路径上的元素避免重复选择,然后收集所有叶子节点上的值,就是所有全排列的结果:
func permute(nums []int) [][]int {
var res [][]int
// 记录回溯算法的递归路径
var track []int
// track 中的元素会被标记为 true
used := make([]bool, len(nums))
backtrack(nums, &res, track, used)
return res
}
// 回溯算法核心函数
func backtrack(nums []int, res *[][]int, track []int, used []bool) {
// base case,到达叶子节点
if len(track) == len(nums) {
// 收集叶子节点上的值
tmp := make([]int, len(track))
copy(tmp, track)
*res = append(*res, tmp)
return
}
// 回溯算法标准框架
for i := 0; i < len(nums); i++ {
// 已经存在 track 中的元素,不能重复选择
if used[i] {
continue
}
// 做选择
used[i] = true
track = append(track, nums[i])
// 进入下一层回溯树
backtrack(nums, res, track, used)
// 取消选择
track = track[:len(track)-1]
used[i] = false
}
}
这样,全排列问题就解决了。
但如果题目不让你算全排列,而是让你算元素个数为 k 的排列,怎么算?
也很简单,改下 backtrack 函数的 base case,仅收集第 k 层的节点值即可:
func backtrack(nums []int, k int) {
// base case,到达第 k 层,收集节点的值
if len(track) == k {
// 第 k 层节点的值就是大小为 k 的排列
res = append(res, append([]int(nil), track...))
return
}
// 回溯算法标准框架
for i := 0; i < len(nums); i++ {
// ...
backtrack(nums, k)
// ...
}
}
子集/组合(元素可重不可复选)
刚才讲的标准子集问题输入的 nums 是没有重复元素的,但如果存在重复元素,怎么处理呢?
力扣第 90 题「子集 II」就是这样一个问题:
给你一个整数数组 nums,其中可能包含重复元素,请你返回该数组所有可能的子集。
比如输入 nums = [1,2,2],你应该输出:
[ [],[1],[2],[1,2],[2,2],[1,2,2] ]
当然,按道理说「集合」不应该包含重复元素的,但既然题目这样问了,我们就忽略这个细节吧,仔细思考一下这道题怎么做才是正事。
就以 nums = [1,2,2] 为例,为了区别两个 2 是不同元素,后面我们写作 nums = [1,2,2']。
按照之前的思路画出子集的树形结构,显然,两条值相同的相邻树枝会产生重复:
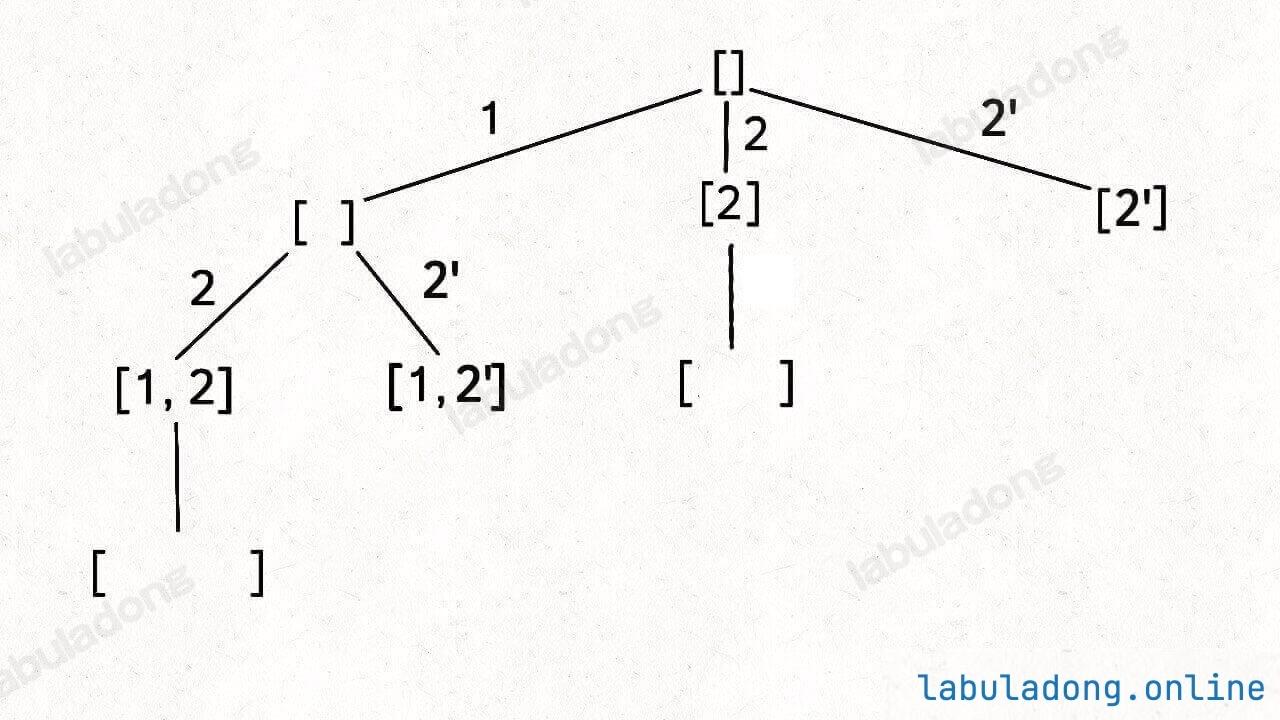
[
[],
[1],[2],[2'],
[1,2],[1,2'],[2,2'],
[1,2,2']
]
你可以看到,[2] 和 [1,2] 这两个结果出现了重复,所以我们需要进行剪枝,如果一个节点有多条值相同的树枝相邻,则只遍历第一条,剩下的都剪掉,不要去遍历:
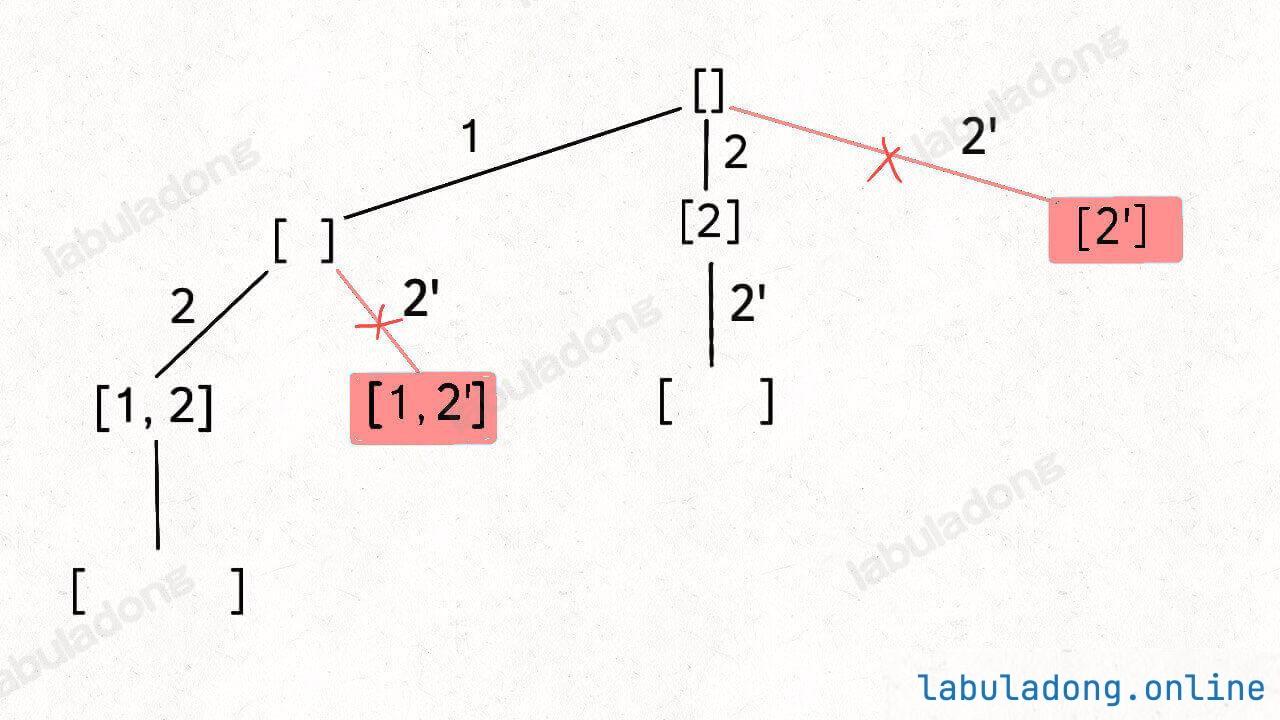
体现在代码上,需要先进行排序,让相同的元素靠在一起,如果发现 nums[i] == nums[i-1],则跳过:
func subsetsWithDup(nums []int) [][]int {
var res [][]int
var track []int
// 先排序,让相同的元素靠在一起
sort.Ints(nums)
backtrack(nums, &track, &res, 0)
return res
}
func backtrack(nums []int, track *[]int, res *[][]int, start int) {
// 前序位置,每个节点的值都是一个子集
tmp := make([]int, len(*track))
copy(tmp, *track)
*res = append(*res, tmp)
for i := start; i < len(nums); i++ {
// 剪枝逻辑,值相同的相邻树枝,只遍历第一条
if i > start && nums[i] == nums[i-1] {
continue
}
*track = append(*track, nums[i])
backtrack(nums, track, res, i+1)
*track = (*track)[:len(*track)-1]
}
}
这段代码和之前标准的子集问题的代码几乎相同,就是添加了排序和剪枝的逻辑。
至于为什么要这样剪枝,结合前面的图应该也很容易理解,这样带重复元素的子集问题也解决了。
我们说了组合问题和子集问题是等价的,所以我们直接看一道组合的题目吧,这是力扣第 40 题「组合总和 II」:
给你输入 candidates 和一个目标和 target,从 candidates 中找出中所有和为 target 的组合。
candidates 可能存在重复元素,且其中的每个数字最多只能使用一次。
说这是一个组合问题,其实换个问法就变成子集问题了:请你计算 candidates 中所有和为 target 的子集。
所以这题怎么做呢?
对比子集问题的解法,只要额外用一个 trackSum 变量记录回溯路径上的元素和,然后将 base case 改一改即可解决这道题:
func combinationSum2(candidates []int, target int) [][]int {
var res [][]int
var track []int
// 记录 track 中的元素之和
var trackSum int
// 先排序,让相同的元素靠在一起
sort.Ints(candidates)
backtrack(candidates, target, 0, &track, &res, &trackSum)
return res
}
// 回溯算法主函数
func backtrack(nums []int, target, start int, track *[]int, res *[][]int, trackSum *int) {
// base case,达到目标和,找到符合条件的组合
if *trackSum == target {
tmp := make([]int, len(*track))
copy(tmp, *track)
*res = append(*res, tmp)
return
}
// base case,超过目标和,直接结束
if *trackSum > target {
return
}
// 回溯算法标准框架
for i := start; i < len(nums); i++ {
// 剪枝逻辑,值相同的树枝,只遍历第一条
if i > start && nums[i] == nums[i-1] {
continue
}
// 做选择
*track = append(*track, nums[i])
*trackSum += nums[i]
// 递归遍历下一层回溯树
backtrack(nums, target, i+1, track, res, trackSum)
// 撤销选择
*track = (*track)[:len(*track)-1]
*trackSum -= nums[i]
}
}
排列(元素可重不可复选)
排列问题的输入如果存在重复,比子集/组合问题稍微复杂一点,我们看看力扣第 47 题「全排列 II」:
给你输入一个可包含重复数字的序列 nums,请你写一个算法,返回所有可能的全排列,函数签名如下:
比如输入 nums = [1,2,2],函数返回:
[ [1,2,2],[2,1,2],[2,2,1] ]
先看解法代码:
func permuteUnique(nums []int) [][]int {
var res [][]int
var track []int
used := make([]bool, len(nums))
// 先排序,让相同的元素靠在一起
sort.Ints(nums)
backtrack(nums, &res, track, used)
return res
}
func backtrack(nums []int, res *[][]int, track []int, used []bool) {
if len(track) == len(nums) {
tmp := make([]int, len(track))
copy(tmp, track)
*res = append(*res, tmp)
return
}
for i := 0; i < len(nums); i++ {
if used[i] {
continue
}
// 新添加的剪枝逻辑,固定相同的元素在排列中的相对位置
if i > 0 && nums[i] == nums[i-1] && !used[i-1] {
continue
}
track = append(track, nums[i])
used[i] = true
backtrack(nums, res, track, used)
track = track[:len(track)-1]
used[i] = false
}
}
你对比一下之前的标准全排列解法代码,这段解法代码只有两处不同:
1、对 nums 进行了排序。
2、添加了一句额外的剪枝逻辑。
类比输入包含重复元素的子集/组合问题,你大概应该理解这么做是为了防止出现重复结果。
但是注意排列问题的剪枝逻辑,和子集/组合问题的剪枝逻辑略有不同:新增了 !used[i - 1] 的逻辑判断。
这个地方理解起来就需要一些技巧性了,且听我慢慢到来。为了方便研究,依然把相同的元素用上标 ’ 以示区别。
假设输入为 nums = [1,2,2'],标准的全排列算法会得出如下答案:
[
[1,2,2'],[1,2',2],
[2,1,2'],[2,2',1],
[2',1,2],[2',2,1]
]
显然,这个结果存在重复,比如 [1,2,2'] 和 [1,2',2] 应该只被算作同一个排列,但被算作了两个不同的排列。
所以现在的关键在于,如何设计剪枝逻辑,把这种重复去除掉?
答案是,保证相同元素在排列中的相对位置保持不变。
比如说 nums = [1,2,2'] 这个例子,我保持排列中 2 一直在 2’ 前面。
这样的话,你从上面 6 个排列中只能挑出 3 个排列符合这个条件:
[ [1,2,2'],[2,1,2'],[2,2',1] ]
这也就是正确答案。
进一步,如果 nums = [1,2,2',2''],我只要保证重复元素 2 的相对位置固定,比如说 2 -> 2' -> 2'',也可以得到无重复的全排列结果。
仔细思考,应该很容易明白其中的原理:
标准全排列算法之所以出现重复,是因为把相同元素形成的排列序列视为不同的序列,但实际上它们应该是相同的;而如果固定相同元素形成的序列顺序,当然就避免了重复。
那么反映到代码上,你注意看这个剪枝逻辑:
// 新添加的剪枝逻辑,固定相同的元素在排列中的相对位置
if (i > 0 && nums[i] == nums[i - 1] && !used[i - 1]) {
// 如果前面的相邻相等元素没有用过,则跳过
continue;
}
// 选择 nums[i]
当出现重复元素时,比如输入 nums = [1,2,2',2''],2' 只有在 2 已经被使用的情况下才会被选择,同理,2'' 只有在 2' 已经被使用的情况下才会被选择,这就保证了相同元素在排列中的相对位置保证固定。
这里拓展一下,如果你把上述剪枝逻辑中的 !used[i - 1] 改成 used[i - 1],其实也可以通过所有测试用例,但效率会有所下降,这是为什么呢?
之所以这样修改不会产生错误,是因为这种写法相当于维护了 2'' -> 2' -> 2 的相对顺序,最终也可以实现去重的效果。
但为什么这样写效率会下降呢?因为这个写法剪掉的树枝不够多。
比如输入 nums = [2,2',2''],产生的回溯树如下:
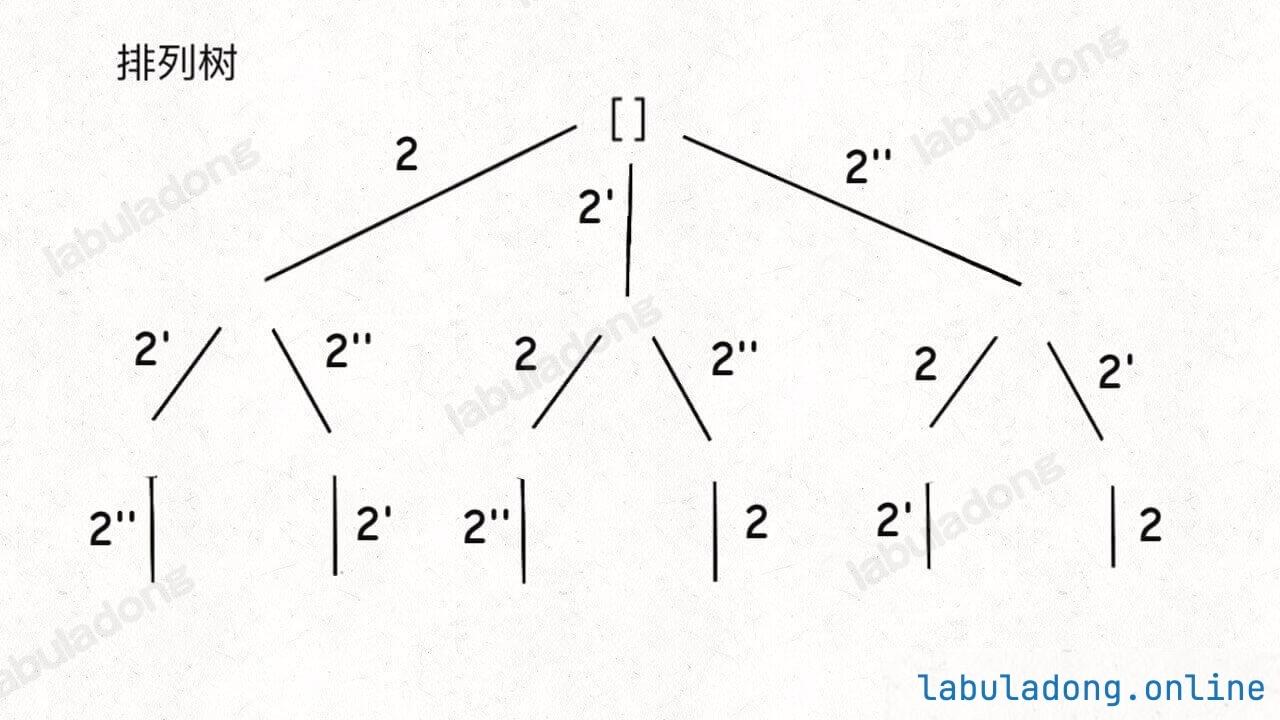
如果用绿色树枝代表 backtrack 函数遍历过的路径,红色树枝代表剪枝逻辑的触发,那么 !used[i - 1] 这种剪枝逻辑得到的回溯树长这样:
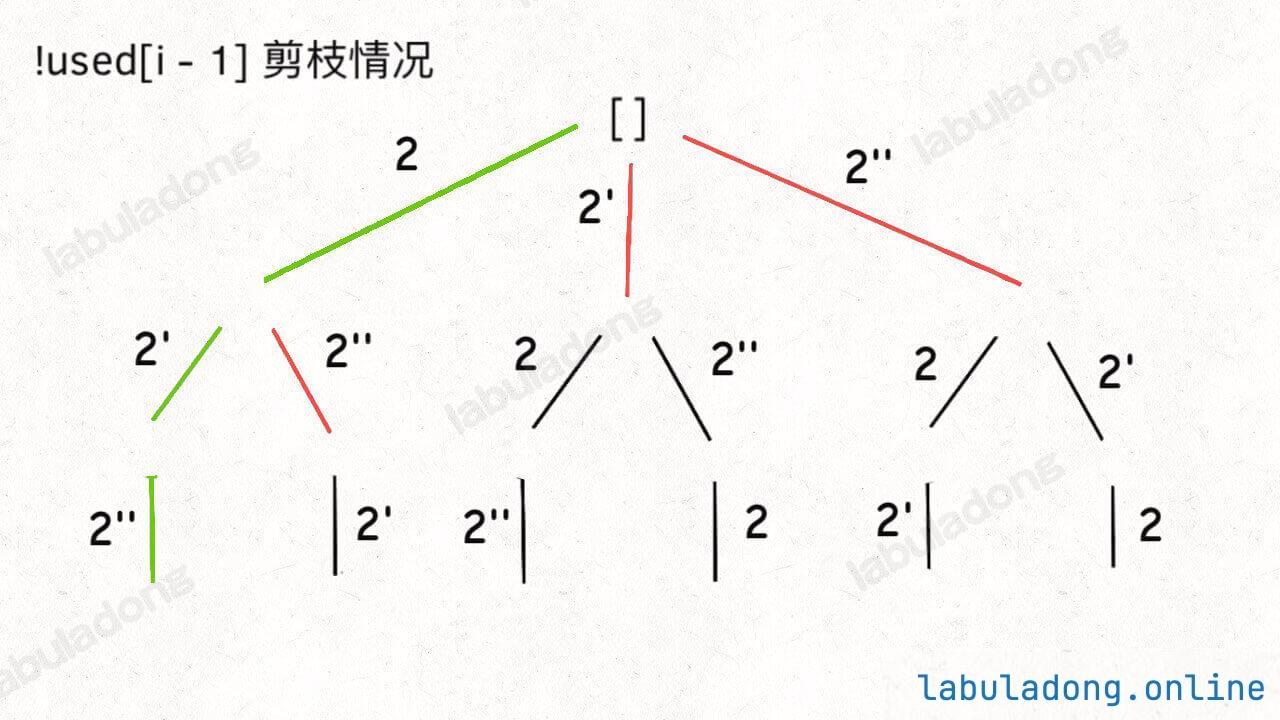
而 used[i - 1]这种剪枝逻辑得到的回溯树如下:
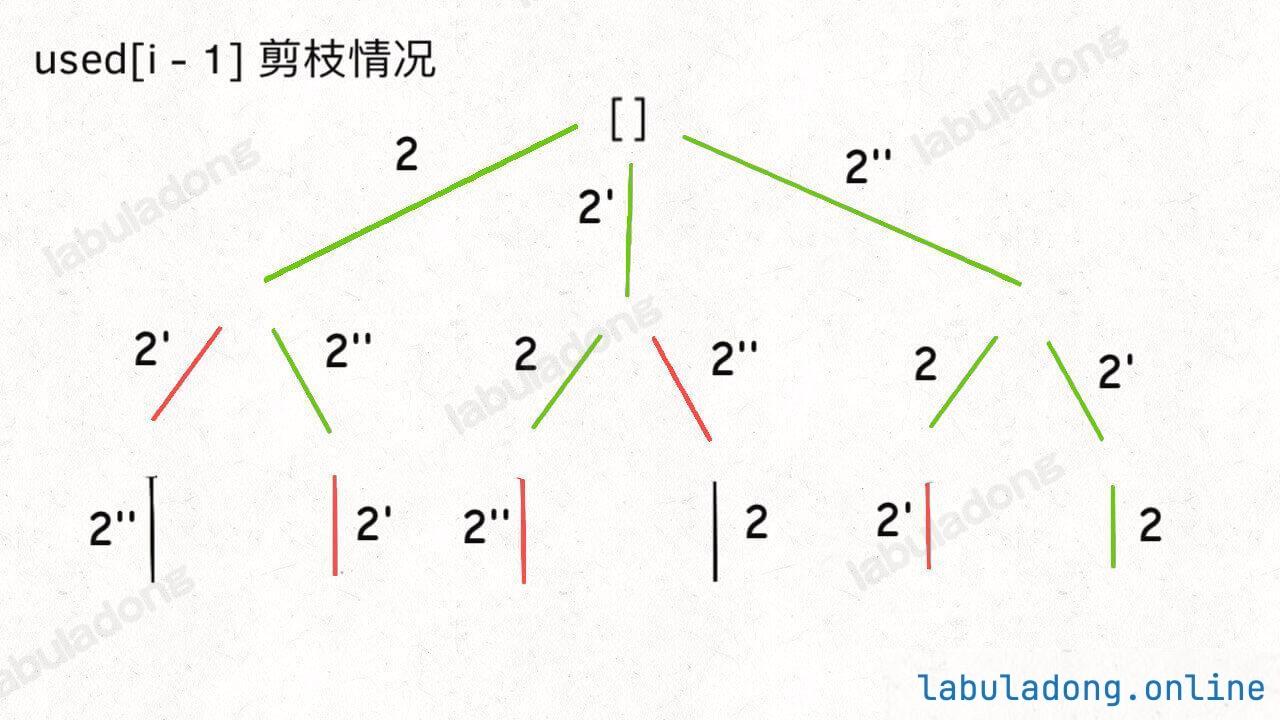
可以看到,!used[i - 1] 这种剪枝逻辑剪得干净利落,而 used[i - 1] 这种剪枝逻辑虽然也能得到无重结果,但它剪掉的树枝较少,存在的无效计算较多,所以效率会差一些。
当然,关于排列去重,也有读者提出别的剪枝思路:
func backtrack(nums []int, track []int) {
if len(track) == len(nums) {
tmp := make([]int, len(track))
copy(tmp, track)
res = append(res, tmp)
return
}
// 记录之前树枝上元素的值
// 题目说 -10 <= nums[i] <= 10,所以初始化为特殊值
prevNum := -666
for i := 0; i < len(nums); i++ {
// 排除不合法的选择
if used[i] {
continue
}
if nums[i] == prevNum {
continue
}
track = append(track, nums[i])
used[i] = true
// 记录这条树枝上的值
prevNum = nums[i]
backtrack(nums, track)
track = track[:len(track)-1]
used[i] = false
}
}
这个思路也是对的,设想一个节点出现了相同的树枝:
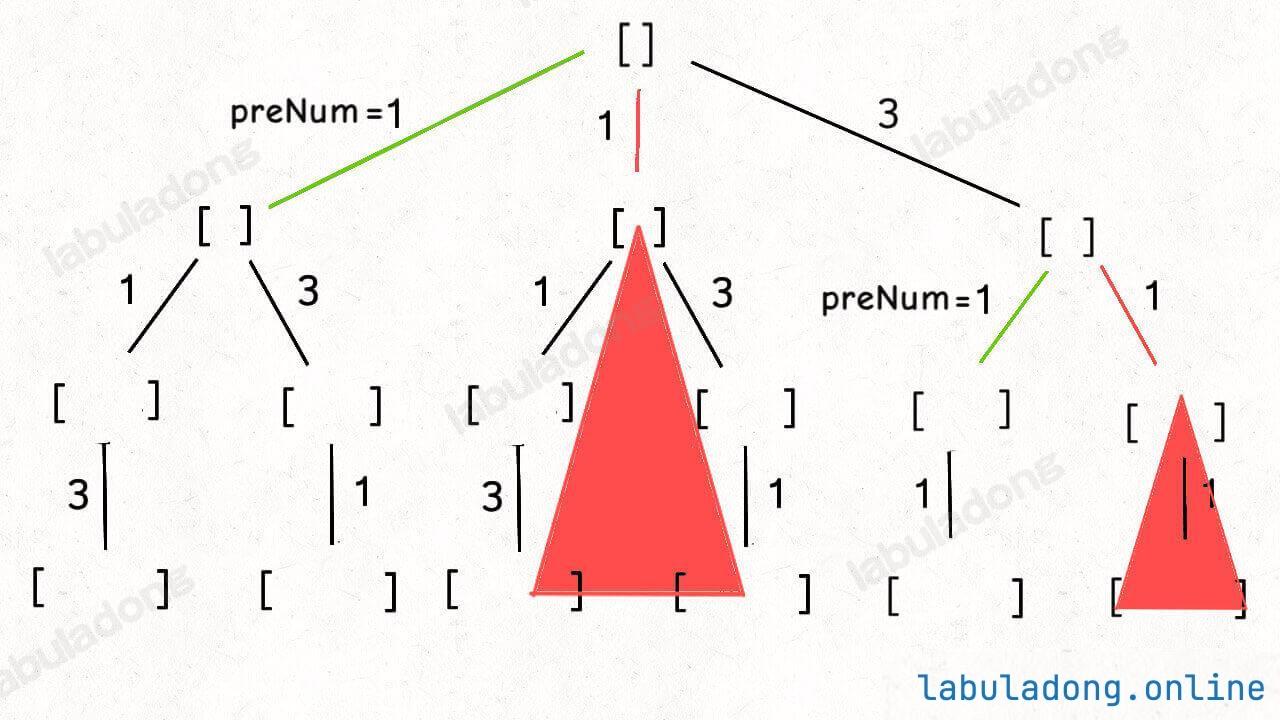
如果不作处理,这些相同树枝下面的子树也会长得一模一样,所以会出现重复的排列。
因为排序之后所有相等的元素都挨在一起,所以只要用 prevNum 记录前一条树枝的值,就可以避免遍历值相同的树枝,从而避免产生相同的子树,最终避免出现重复的排列。
好了,这样包含重复输入的排列问题也解决了。
子集/组合(元素无重可复选)
终于到了最后一种类型了:输入数组无重复元素,但每个元素可以被无限次使用。
直接看力扣第 39 题「组合总和」:
给你一个无重复元素的整数数组 candidates 和一个目标和 target,找出 candidates 中可以使数字和为目标数 target 的所有组合。candidates 中的每个数字可以无限制重复被选取。
比如输入 candidates = [1,2,3], target = 3,算法应该返回:
[ [1,1,1],[1,2],[3] ]
这道题说是组合问题,实际上也是子集问题:candidates 的哪些子集的和为 target?
想解决这种类型的问题,也得回到回溯树上,我们不妨先思考思考,标准的子集/组合问题是如何保证不重复使用元素的?
答案在于 backtrack 递归时输入的参数 start:
// 无重组合的回溯算法框架
func backtrack(nums []int, start int) {
for i := start; i < len(nums); i++ {
// ...
// 递归遍历下一层回溯树,注意参数
backtrack(nums, i + 1)
// ...
}
}
这个 i 从 start 开始,那么下一层回溯树就是从 start + 1 开始,从而保证 nums[start] 这个元素不会被重复使用:
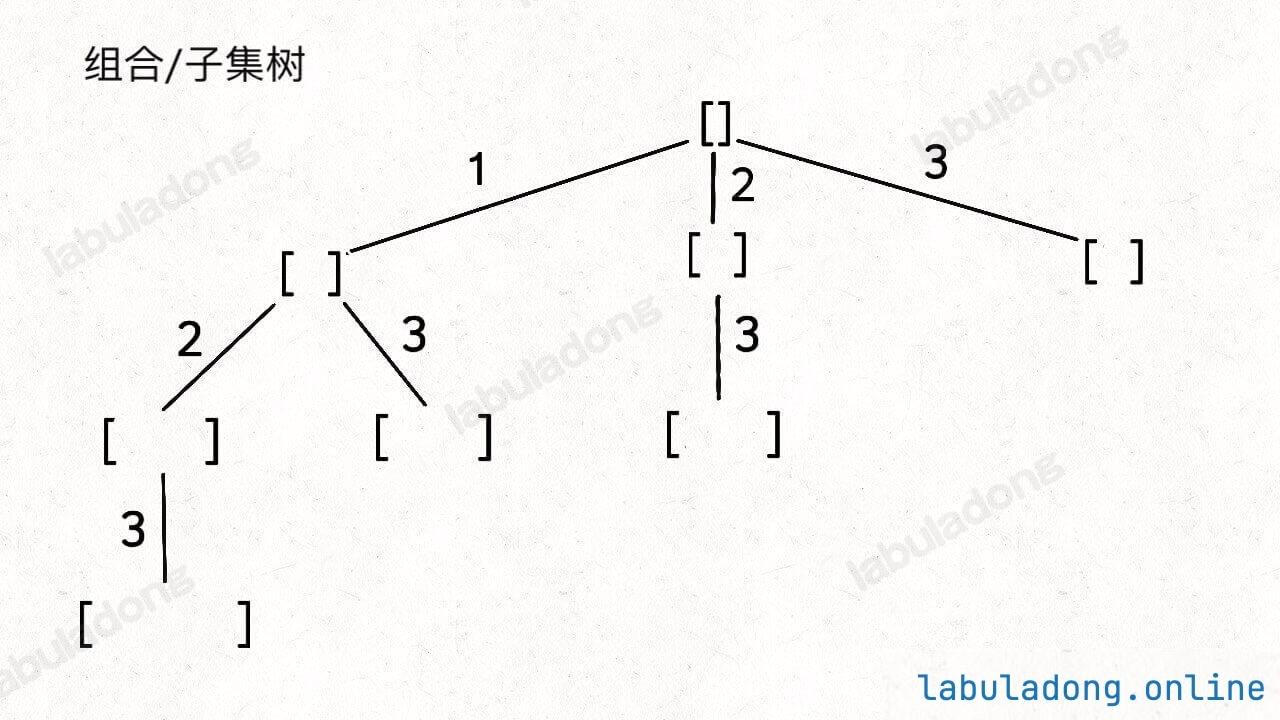
那么反过来,如果我想让每个元素被重复使用,我只要把 i + 1 改成 i 即可:
// 可重组合的回溯算法框架
func backtrack(nums []int, start int) {
for i := start; i < len(nums); i++ {
// ...
// 递归遍历下一层回溯树,注意参数
backtrack(nums, i)
// ...
}
}
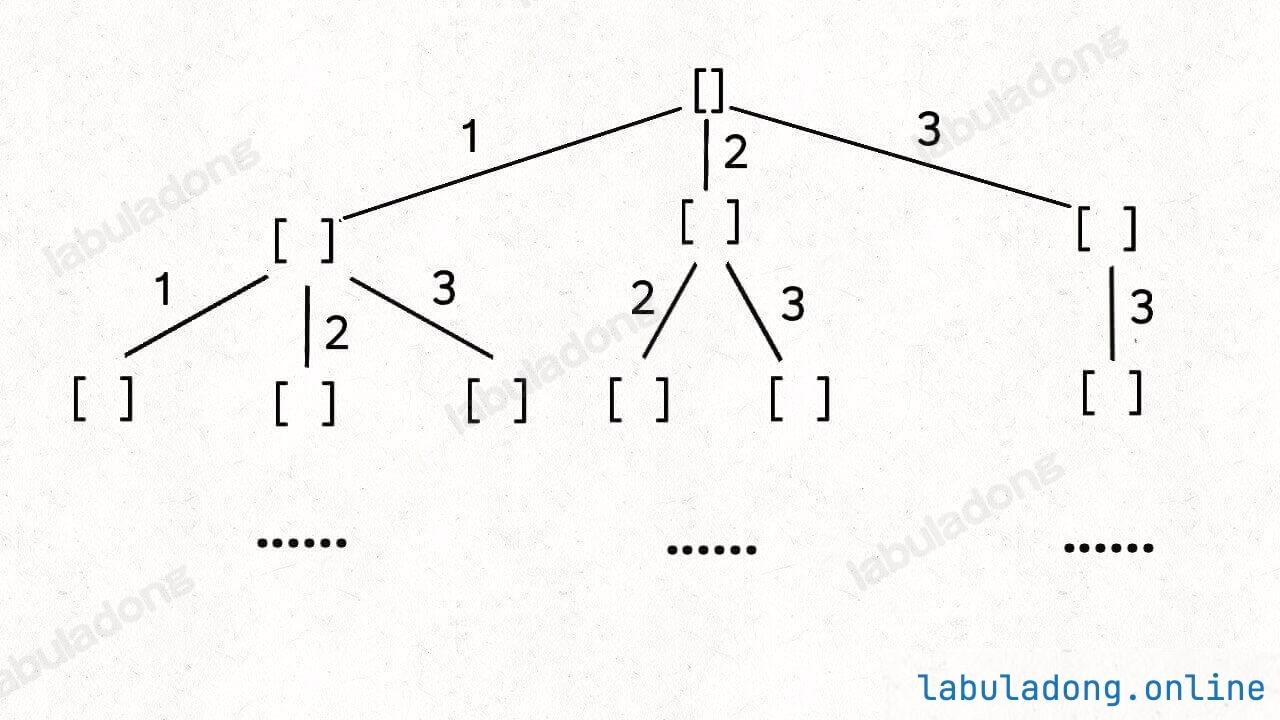
当然,这样这棵回溯树会永远生长下去,所以我们的递归函数需要设置合适的 base case 以结束算法,即路径和大于 target 时就没必要再遍历下去了。
这道题的解法代码如下:
func combinationSum(candidates []int, target int) [][]int {
var res [][]int
// 记录回溯的路径
var track []int
// 记录 track 中的路径和
trackSum := 0
var backtrack func([]int, int)
backtrack = func(nums []int, start int) {
// base case,找到目标和,记录结果
if trackSum == target {
tmp := make([]int, len(track))
copy(tmp, track)
res = append(res, tmp)
return
}
// base case,超过目标和,停止向下遍历
if trackSum > target {
return
}
// 回溯算法标准框架
for i := start; i < len(nums); i++ {
// 选择 nums[i]
trackSum += nums[i]
track = append(track, nums[i])
// 递归遍历下一层回溯树
// 同一元素可重复使用,注意参数
backtrack(nums, i)
// 撤销选择 nums[i]
trackSum -= nums[i]
track = track[:len(track)-1]
}
}
backtrack(candidates, 0)
return res
}
排列(元素无重可复选)
力扣上没有题目直接考察这个场景,我们不妨先想一下,nums 数组中的元素无重复且可复选的情况下,会有哪些排列?
比如输入 nums = [1,2,3],那么这种条件下的全排列共有 3^3 = 27 种:
[
[1,1,1],[1,1,2],[1,1,3],[1,2,1],[1,2,2],[1,2,3],[1,3,1],[1,3,2],[1,3,3],
[2,1,1],[2,1,2],[2,1,3],[2,2,1],[2,2,2],[2,2,3],[2,3,1],[2,3,2],[2,3,3],
[3,1,1],[3,1,2],[3,1,3],[3,2,1],[3,2,2],[3,2,3],[3,3,1],[3,3,2],[3,3,3]
]
标准的全排列算法利用 used 数组进行剪枝,避免重复使用同一个元素。如果允许重复使用元素的话,直接放飞自我,去除所有 used 数组的剪枝逻辑就行了。
那这个问题就简单了,代码如下:
func permuteRepeat(nums []int) [][]int {
var res [][]int
var track []int
backtrack(nums, &res, track)
return res
}
// 回溯算法核心函数
func backtrack(nums []int, res *[][]int, track []int) {
// base case,到达叶子节点
if len(track) == len(nums) {
// 收集叶子节点上的值
tmp := make([]int, len(track))
copy(tmp, track)
*res = append(*res, tmp)
return
}
// 回溯算法标准框架
for i := 0; i < len(nums); i++ {
// 做选择
track = append(track, nums[i])
// 进入下一层回溯树
backtrack(nums, res, track)
// 取消选择
track = track[:len(track)-1]
}
}
至此,排列/组合/子集问题的九种变化就都讲完了。
最后总结
来回顾一下排列/组合/子集问题的三种形式在代码上的区别。
由于子集问题和组合问题本质上是一样的,无非就是 base case 有一些区别,所以把这两个问题放在一起看。
形式一、元素无重不可复选,即 nums 中的元素都是唯一的,每个元素最多只能被使用一次,backtrack 核心代码如下:
// 组合/子集问题回溯算法框架
func backtrack(nums []int, start int) {
// 回溯算法标准框架
for i := start; i < len(nums); i++ {
// 做选择
track = append(track, nums[i])
// 注意参数
backtrack(nums, i+1)
// 撤销选择
track = track[:len(track)-1]
}
}
// 排列问题回溯算法框架
func backtrack(nums []int) {
for i := 0; i < len(nums); i++ {
// 剪枝逻辑
if used[i] {
continue
}
// 做选择
used[i] = true
track = append(track, nums[i])
backtrack(nums)
// 撤销选择
track = track[:len(track)-1]
used[i] = false
}
}
形式二、元素可重不可复选,即 nums 中的元素可以存在重复,每个元素最多只能被使用一次,其关键在于排序和剪枝,backtrack 核心代码如下:
sort.Ints(nums)
// 组合/子集问题回溯算法框架
func backtrack(nums []int, start int) {
// 回溯算法标准框架
for i := start; i < len(nums); i++ {
// 剪枝逻辑,跳过值相同的相邻树枝
if i > start && nums[i] == nums[i-1] {
continue
}
// 做选择
track = append(track, nums[i])
// 注意参数
backtrack(nums, i+1)
// 撤销选择
track = track[:len(track)-1]
}
}
sort.Ints(nums)
// 排列问题回溯算法框架
func backtrack(nums []int) {
for i := 0; i < len(nums); i++ {
// 剪枝逻辑
if used[i] {
continue
}
// 剪枝逻辑,固定相同的元素在排列中的相对位置
if i > 0 && nums[i] == nums[i-1] && !used[i-1] {
continue
}
// 做选择
used[i] = true
track = append(track, nums[i])
backtrack(nums)
// 撤销选择
track = track[:len(track)-1]
used[i] = false
}
}
形式三、元素无重可复选,即 nums 中的元素都是唯一的,每个元素可以被使用若干次,只要删掉去重逻辑即可,backtrack 核心代码如下:
// 组合/子集问题回溯算法框架
func backtrack(nums []int, start int) {
// 回溯算法标准框架
for i := start; i < len(nums); i++ {
// 做选择
track = append(track, nums[i])
// 注意参数
backtrack(nums, i)
// 撤销选择
track = track[:len(track)-1]
}
}
// 排列问题回溯算法框架
func backtrack(nums []int) {
for i := 0; i < len(nums); i++ {
// 做选择
track = append(track, nums[i])
backtrack(nums)
// 撤销选择
track = track[:len(track)-1]
}
}
只要从树的角度思考,这些问题看似复杂多变,实则改改 base case 就能解决,这也是为什么我在 学习算法和数据结构的框架思维 和 手把手刷二叉树(纲领篇) 中强调树类型题目重要性的原因。
如果你能够看到这里,真得给你鼓掌,相信你以后遇到各种乱七八糟的算法题,也能一眼看透它们的本质,以不变应万变。另外,考虑到篇幅,本文并没有对这些算法进行复杂度的分析,你可以使用我在 算法时空复杂度分析实用指南 讲到的复杂度分析方法尝试自己分析它们的复杂度。