BFS 算法解题套路框架
我多次强调,DFS/回溯/BFS 这类算法,本质上就是把具体的问题抽象成树结构,然后遍历这棵树进行暴力穷举,所以这些穷举算法的代码本质上就是树的遍历代码。
梳理一下这里面的因果关系:
DFS/回溯算法的本质就是递归遍历一棵穷举树(多叉树),而多叉树的递归遍历又是从二叉树的递归遍历衍生出来的。所以我说 DFS/回溯算法的本质是二叉树的递归遍历。
BFS 算法的本质就是遍历一幅图,下面你就会看到了,BFS 的算法框架就是 图结构的 DFS/BFS 遍历 中遍历图节点的算法代码。
而图的遍历算法其实就是多叉树的遍历算法加了个 visited 数组防止死循环;多叉树的遍历算法又是从二叉树遍历算法衍生出来的。所以我说 BFS 算法的本质就是二叉树的层序遍历。
为啥 BFS 算法经常用来求解最短路径问题?我在 DFS 和 BFS 的适用场景 中用二叉树的最小深度这道例题详细说明过。
其实所谓的最短路径,都可以类比成二叉树最小深度这类问题(寻找距离根节点最近的叶子节点),递归遍历必须要遍历整棵树的所有节点才能找到目标节点,而层序遍历不需要遍历所有节点就能搞定,所以层序遍历适合解决这类最短路径问题。
这么梳理应该够清楚了吧?
所以阅读本文前,需要确保你学过前面的 二叉树的递归/层序遍历、 多叉树的递归/层序遍历 和 图结构的 DFS/BFS 遍历,先把这几种基本数据结构的遍历算法玩明白,其他的算法都会很容易理解。
本文的重点在于,教会你如何对具体的算法问题进行抽象和转化,然后套用 BFS 算法框架进行求解。
在真实的面试笔试题目中,一般不是直接让你遍历树/图这种标准数据结构,而是给你一个具体的场景题,你需要把具体的场景抽象成一个标准的图/树结构,然后利用 BFS 算法穷举得出答案。
比方说给你一个迷宫游戏,请你计算走到出口的最小步数?如果这个迷宫还包含传送门,可以瞬间传送到另一个位置,那么最小步数又是多少?
再比如说两个单词,要求你通过某些替换,把其中一个变成另一个,每次可以替换/删除/插入一个字符,最少要操作几次?
再比如说连连看游戏,两个方块消除的条件不仅仅是图案相同,还得保证两个方块之间的最短连线不能多于两个拐点。你玩连连看,点击两个坐标,游戏是如何判断它俩的最短连线有几个拐点的?
你看上面这些例子,是不是感觉和我们前面学习的树/图结构完全扯不上关系?但实际上只要稍加抽象,它们就是树/图结构的遍历,实在是太简单枯燥了。
下面用几道例题来讲解 BFS 的套路框架,以后再也不要觉得这类问题难解决了。
算法框架
BFS 的算法框架其实就是 图结构的 DFS/BFS 遍历 中给出的 BFS 遍历图结构的代码,共有三种写法。
对于实际的 BFS 算法问题,第一种写法最简单,但局限性太大,不常用;第二种写法最常用,中等难度的 BFS 算法题基本都可以用这种写法解决;第三种写法稍微复杂一点,但灵活性最高,可能会在一些难度较大的的 BFS 问题中用到。在下一章的 BFS 算法习题章节 中,会有一些难度更大的题目使用第三种写法,到时候你可以自己尝试。
本文的例题都是中等难度,所以本文给出的解法都以第二种写法为准:
// 从 s 开始 BFS 遍历图的所有节点,且记录遍历的步数
// 当走到目标节点 target 时,返回步数
func bfs(graph Graph, s int, target int) int {
visited := make([]bool, graph.size())
q := []int{s}
visited[s] = true
// 记录从 s 开始走到当前节点的步数
step := 0
for len(q) > 0 {
sz := len(q)
for i := 0; i < sz; i++ {
cur := q[0]
q = q[1:]
fmt.Printf("visit %d at step %d\n", cur, step)
// 判断是否到达终点
if cur == target {
return step
}
// 将邻居节点加入队列,向四周扩散搜索
for _, to := range neighborsOf(cur) {
if !visited[to] {
q = append(q, to)
visited[to] = true
}
}
}
step++
}
// 如果走到这里,说明在图中没有找到目标节点
return -1
}
上面这个代码框架几乎就是从
图结构的 DFS/BFS 遍历 中复制过来的,只不过添加了一个 target 参数,当第一次走到 target 时,直接结束算法并返回走过的步数。
下面我们用几个具体的例题来看看如何运用这个框架。
滑动谜题
力扣第 773 题「滑动谜题」就是一个可以运用 BFS 框架解决的题目,题目的要求如下:
给你一个 2x3 的滑动拼图,用一个 2x3 的数组 board 表示。拼图中有数字 0~5 六个数,其中数字 0 就表示那个空着的格子,你可以移动其中的数字,当 board 变为 [[1,2,3],[4,5,0]] 时,赢得游戏。
请你写一个算法,计算赢得游戏需要的最少移动次数,如果不能赢得游戏,返回 -1。
比如说输入的二维数组 board = [[4,1,2],[5,0,3]],算法应该返回 5:
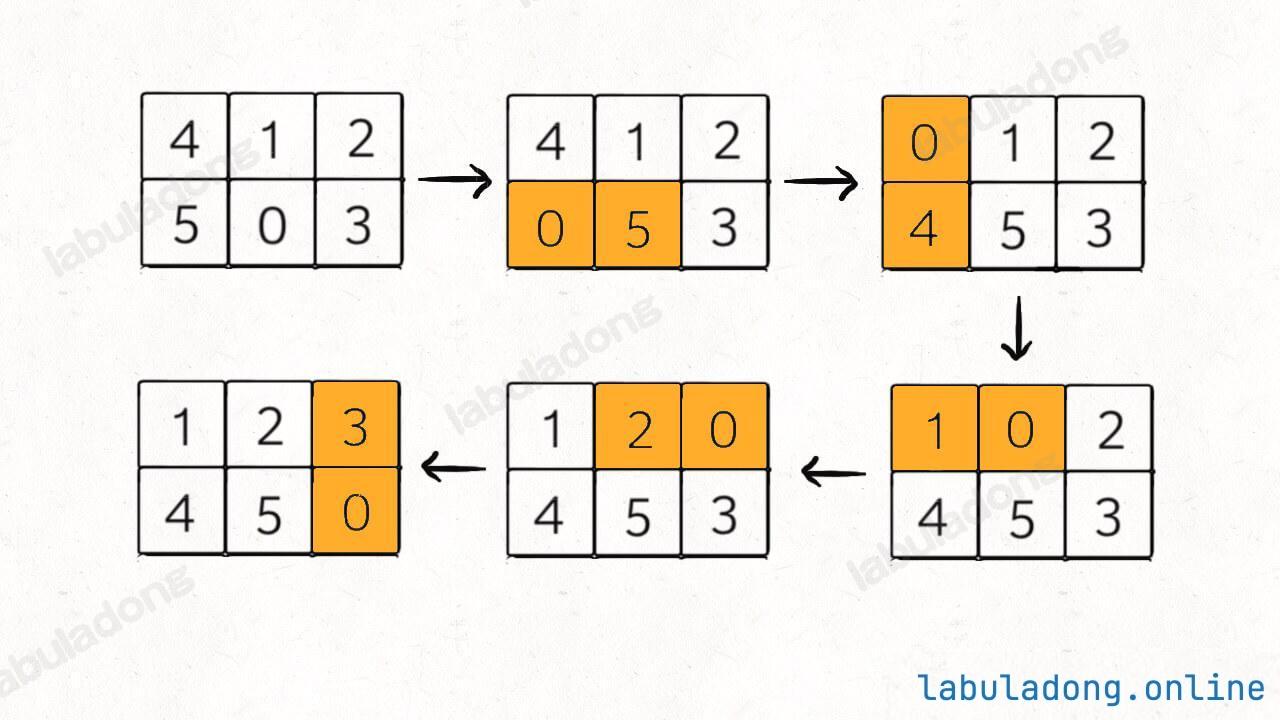
如果输入的是 board = [[1,2,3],[5,4,0]],则算法返回 -1,因为这种局面下无论如何都不能赢得游戏。
我感觉这题还挺有意思的,小时候玩过类似的拼图游戏,比如华容道:

你需要移动这些方块,想办法让曹操从初始位置移动到最下方的出口位置。
华容道应该比这道题更难一些,因为力扣的这道题中每个方块的大小可以看作是相同的,而华容道中每个方块的大小还不一样。
回到这道题,我们如何把这道题抽象成树/图的结构,从而用 BFS 算法框架来解决呢?
其实棋盘的初始状态就可以认为是起点:
[[2,4,1],
[5,0,3]]
我们最终的目标状态是把棋盘变成这样:
[[1,2,3],
[4,5,0]]
那么这就可以认为是终点。
现在这个问题不就成为了一个图的问题了吗?题目问的其实就是从起点到终点所需的最短路径是多少嘛。
起点的邻居节点是谁?把数字 0 和上下左右的数字进行交换,其实就是起点的四个邻居节点嘛(由于本题中棋盘的大小是 2x3,所以索引边界内的实际邻居节点会小于四个):
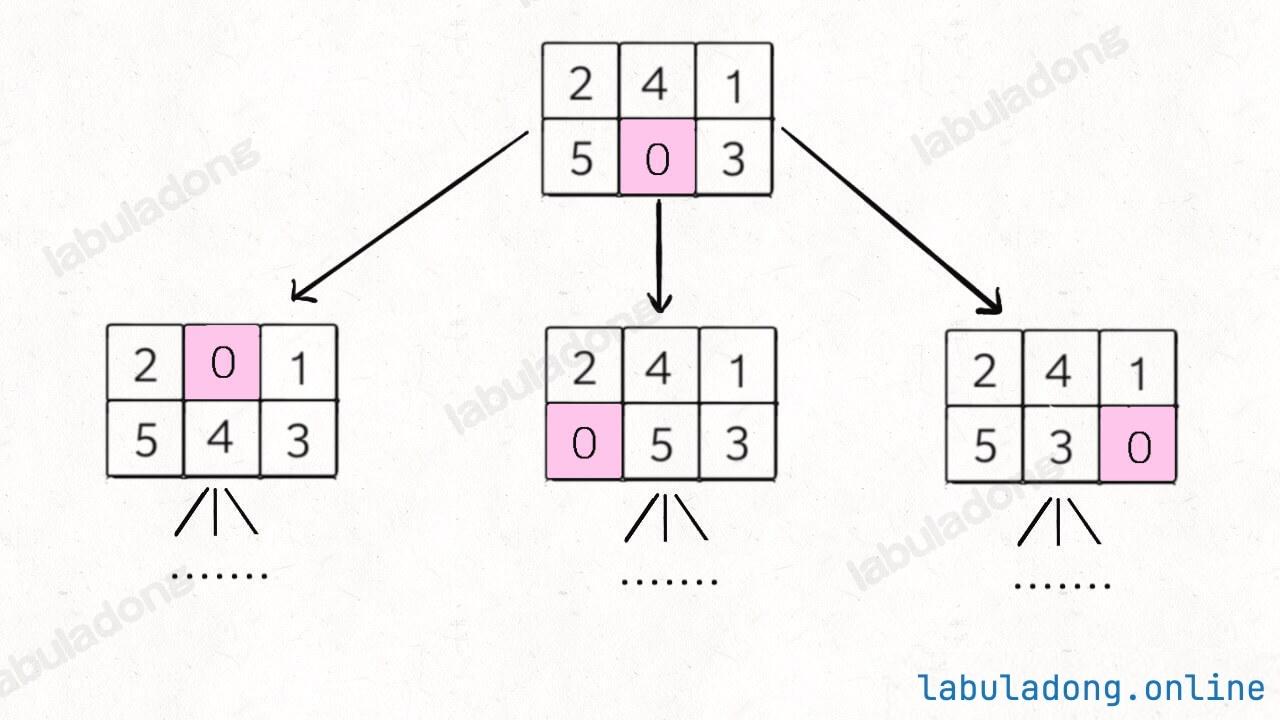
以此类推,这四个邻居节点还有各自的四个邻居节点,那这不就是一幅图结构吗?
那么我从起点开始使用 BFS 算法遍历这幅图,第一次到达终点时,走过的步数就是答案。
伪码如下:
int bfs(int[][] board, int[][] target) {
Queue<int[][]> q = new LinkedList<>();
HashSet visited = new HashSet<>();
// 将起点加入队列
q.offer(board);
visited.add(board);
int step = 0;
while (!q.isEmpty()) {
int sz = q.size();
for (int i = 0; i < sz; i++) {
int[][] cur = q.poll();
// 判断是否到达终点
if (cur == target) {
return step;
}
// 将当前节点的邻居节点加入队列
for (int[][] neighbor : getNeighbors(cur)) {
if (!visited.contains(neighbor)) {
q.offer(neighbor);
visited.add(neighbor);
}
}
}
step++;
}
return -1;
}
List<int[][]> getNeighbors(int[][] board) {
// 将 board 中的数字 0 和上下左右的数字进行交换,得到 4 个邻居节点
}
对于这道题,我们抽象出来的图结构也是会包含环的,所以需要一个 visited 数组记录已经走过的节点,避免成环导致死循环。
比如说我从 [[2,4,1],[5,0,3]] 节点开始,数字 0 向右移动得到新节点 [[2,4,1],[5,3,0]],但是这个新节点中的 0 也可以向左移动的,又会回到 [[2,4,1],[5,0,3]],这其实就是成环。我们也需要一个 visited 哈希集合来记录已经走过的节点,防止成环导致的死循环。
还有一个问题,这道题中 board 是一个二维数组,我们在 哈希表/哈希集合原理 中介绍过,二维数组这种可变数据结构是无法直接加入哈希集合的。
所以我们还要再用一点技巧,想办法把二维数组转化成一个不可变类型才能存到哈希集合中。常见的解决方案是把二维数组序列化成一个字符串,这样就可以直接存入哈希集合了。
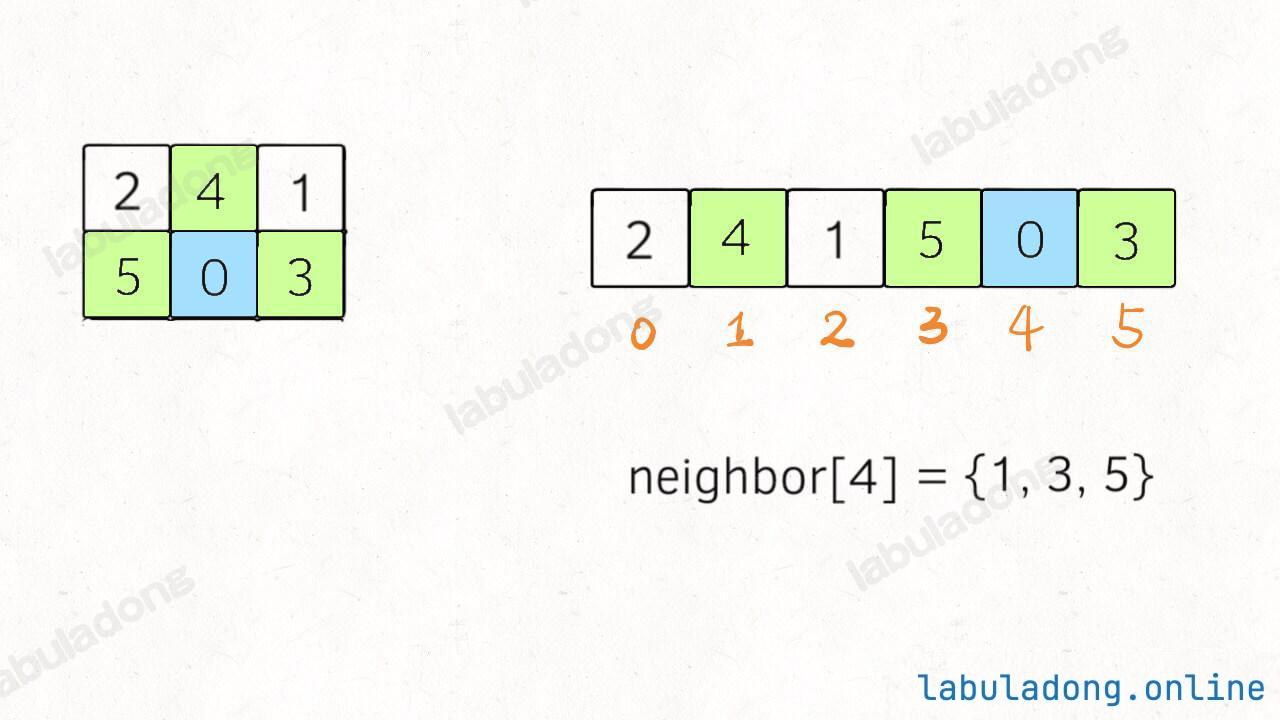
其中比较有技巧性的点在于,二维数组有「上下左右」的概念,压缩成一维的字符串后后,还怎么把数字 0 和上下左右的数字进行交换?
对于这道题,题目说输入的数组大小都是 2 x 3,所以我们可以直接手动写出来这个映射:
// 记录一维字符串相邻索引
neighbor := [][]int{
{1, 3},
{0, 4, 2},
{1, 5},
{0, 4},
{3, 1, 5},
{4, 2},
}
这个映射的含义就是,在一维字符串中,索引 i 在二维数组中的的相邻索引为 neighbor[i]:
如果是 m x n 的二维数组,怎么办?
对于一个 m x n 的二维数组,手写它的一维索引映射肯定不现实了,需要用代码生成它的一维索引映射。
观察上图就能发现,如果二维数组中的某个元素 e 在一维数组中的索引为 i,那么 e 的左右相邻元素在一维数组中的索引就是 i - 1 和 i + 1,而 e 的上下相邻元素在一维数组中的索引就是 i - n 和 i + n,其中 n 为二维数组的列数。
这样,对于 m x n 的二维数组,我们可以写一个函数来生成它的 neighbor 索引映射:
```go
func generateNeighborMapping(m, n int) [][]int {
neighbor := make([][]int, m*n)
for i := 0; i < m*n; i++ {
neighbors := make([]int, 0)
// 如果不是第一列,有左侧邻居
if i % n != 0 {
neighbors = append(neighbors, i-1)
}
// 如果不是最后一列,有右侧邻居
if i % n != n-1 {
neighbors = append(neighbors, i+1)
}
// 如果不是第一行,有上方邻居
if i-n >= 0 {
neighbors = append(neighbors, i-n)
}
// 如果不是最后一行,有下方邻居
if i+n < m*n {
neighbors = append(neighbors, i+n)
}
neighbor[i] = neighbors
}
return neighbor
}
```
这样,无论数字 0 在哪里,都可以通过这个索引映射得到它的相邻索引进行交换了。下面是完整的代码实现:
func slidingPuzzle(board [][]int) int {
target := "123450"
// 将 2x3 的数组转化成字符串作为 BFS 的起点
start := ""
for i := 0; i < len(board); i++ {
for j := 0; j < len(board[0]); j++ {
start += string(rune(board[i][j] + '0'))
}
}
// ****** BFS 算法框架开始 ******
queue := []string{start}
visited := make(map[string]bool)
visited[start] = true
step := 0
for len(queue) > 0 {
sz := len(queue)
for i := 0; i < sz; i++ {
cur := queue[0]
queue = queue[1:]
// 判断是否达到目标局面
if cur == target {
return step
}
// 将数字 0 和相邻的数字交换位置
for _, neighbor := range getNeighbors(cur) {
// 防止走回头路
if !visited[neighbor] {
queue = append(queue, neighbor)
visited[neighbor] = true
}
}
}
step++
}
// ****** BFS 算法框架结束 ******
return -1
}
func getNeighbors(board string) []string {
// 记录一维字符串的相邻索引
mapping := [][]int{
{1, 3},
{0, 4, 2},
{1, 5},
{0, 4},
{3, 1, 5},
{4, 2},
}
idx := strings.Index(board, "0")
neighbors := []string{}
for _, adj := range mapping[idx] {
newBoard := swap(board, idx, adj)
neighbors = append(neighbors, newBoard)
}
return neighbors
}
func swap(board string, i, j int) string {
chars := []rune(board)
chars[i], chars[j] = chars[j], chars[i]
return string(chars)
}
这道题就解决了。你会发现 BFS 算法本身的写法都是固定的套路,这道题的难点其实在于将题目转化为 BFS 穷举的模型,然后用合理的方法将多维数组转化成字符串,以便哈希集合记录访问过的节点。
下面再看一道实际场景题。
解开密码锁的最少次数
来看力扣第 752 题「打开转盘锁」,比较有意思:
题目中描述的就是我们生活中常见的那种密码锁,如果没有任何约束,最少的拨动次数很好算。比方说想拨到 “1234”,那一个个数字拨动就可以了,最少的拨动次数就是 1 + 2 + 3 + 4 = 10 次。
但现在的难点就在于,在拨动密码锁的过程中不能出现 deadends,这样就有一些难度了。如果遇到了 deadends,你该怎么处理,才能使得总的拨动次数最少呢?
千万不要陷入细节,尝试去想各种具体的情况。要知道算法的本质就是穷举,我们直接从 "0000" 开始暴力穷举,把所有可能的拨动情况都穷举出来,难道还怕找不到最少的拨动次数么?
第一步,我们不管所有的限制条件,不管 deadends 和 target 的限制,就思考一个问题:如果让你设计一个算法,穷举所有可能的密码组合,你怎么做?
就从 "0000" 开始,如果你只转一下锁,有几种可能?总共有 4 个位置,每个位置可以向上转,也可以向下转,也就是可以穷举出 "1000", "9000", "0100", "0900"... 共 8 种密码。
然后,再以这 8 种密码作为基础,其中每个密码又可以转动一下衍生出 8 种密码,以此类推…
心里那棵递归树出来没有?应该是一棵八叉树,每个节点都有 8 个子节点,向下衍生。
下面这段伪码就描述了上述思路,用层序遍历一棵八叉树:
// 将 s[j] 向上拨动一次
func plusOne(s string, j int) string {
ch := []byte(s)
if ch[j] == '9' {
ch[j] = '0'
} else {
ch[j] += 1
}
return string(ch)
}
// 将 s[i] 向下拨动一次
func minusOne(s string, j int) string {
ch := []byte(s)
if ch[j] == '0' {
ch[j] = '9'
} else {
ch[j] -= 1
}
return string(ch)
}
// BFS 框架,寻找最少的拨动次数
func BFS(target string) int {
q := []string{"0000"}
step := 0
for len(q) > 0 {
sz := len(q)
// 将当前队列中的所有节点向周围扩散
for i := 0; i < sz; i++ {
cur := q[0]
q = q[1:]
// 判断是否到达终点
if cur == target {
return step
}
// 将一个节点的相邻节点加入队列
for _, neighbor := range getNeighbors(cur) {
q = append(q, neighbor)
}
}
// 在这里增加步数
step++
}
return -1
}
// 将 s 的每一位向上拨动一次或向下拨动一次,8 种相邻密码
func getNeighbors(s string) []string {
neighbors := []string{}
for i := 0; i < 4; i++ {
neighbors = append(neighbors, plusOne(s, i))
neighbors = append(neighbors, minusOne(s, i))
}
return neighbors
}
这个代码已经可以穷举所有可能的密码组合了,但是还有些问题需要解决。
1、会走回头路,我们可以从 "0000" 拨到 "1000",但是等从队列拿出 "1000" 时,还会拨出一个 "0000",这样的话会产生死循环。
这个问题很好解决,其实就是成环了嘛,我们用一个 visited 集合记录已经穷举过的密码,再次遇到时,不要再加到队列里就行了。
2、没有对 deadends 进行处理,按道理这些「死亡密码」是不能出现的。
这个问题也好处理,额外用一个 deadends 集合记录这些死亡密码,凡是遇到这些密码,不要加到队列里就行了。
或者还可以更简单一些,直接把 deadends 中的死亡密码作为 visited 集合的初始元素,这样也可以达到目的。
下面是完整的代码实现:
func openLock(deadends []string, target string) int {
// 记录需要跳过的死亡密码
deads := make(map[string]struct{})
for _, s := range deadends {
deads[s] = struct{}{}
}
if _, found := deads["0000"]; found {
return -1
}
// 记录已经穷举过的密码,防止走回头路
visited := make(map[string]struct{})
q := make([]string, 0)
// 从起点开始启动广度优先搜索
step := 0
q = append(q, "0000")
visited["0000"] = struct{}{}
for len(q) > 0 {
sz := len(q)
// 将当前队列中的所有节点向周围扩散
for i := 0; i < sz; i++ {
cur := q[0]
q = q[1:]
// 判断是否到达终点
if cur == target {
return step
}
// 将一个节点的合法相邻节点加入队列
for _, neighbor := range getNeighbors(cur) {
if _, found := visited[neighbor]; !found {
if _, dead := deads[neighbor]; !dead {
q = append(q, neighbor)
visited[neighbor] = struct{}{}
}
}
}
}
// 在这里增加步数
step++
}
// 如果穷举完都没找到目标密码,那就是找不到了
return -1
}
// 将 s[j] 向上拨动一次
func plusOne(s string, j int) string {
ch := []rune(s)
if ch[j] == '9' {
ch[j] = '0'
} else {
ch[j]++
}
return string(ch)
}
// 将 s[i] 向下拨动一次
func minusOne(s string, j int) string {
ch := []rune(s)
if ch[j] == '0' {
ch[j] = '9'
} else {
ch[j]--
}
return string(ch)
}
// 将 s 的每一位向上拨动一次或向下拨动一次,8 种相邻密码
func getNeighbors(s string) []string {
neighbors := make([]string, 0)
for i := 0; i < 4; i++ {
neighbors = append(neighbors, plusOne(s, i))
neighbors = append(neighbors, minusOne(s, i))
}
return neighbors
}
双向 BFS 优化
下面再介绍一种 BFS 算法的优化思路:双向 BFS,可以提高 BFS 搜索的效率。
你把这种技巧当做扩展阅读就行,在一般的面试笔试题中,普通的 BFS 算法已经够用了,如果遇到超时无法通过,或者面试官的追问,可以考虑解法是否需要双向 BFS 优化。
双向 BFS 就是从标准的 BFS 算法衍生出来的:
传统的 BFS 框架是从起点开始向四周扩散,遇到终点时停止;而双向 BFS 则是从起点和终点同时开始扩散,当两边有交集的时候停止。
为什么这样能够能够提升效率呢?
就好比有 A 和 B 两个人,传统 BFS 就相当于 A 出发去找 B,而 B 待在原地不动;双向 BFS 则是 A 和 B 一起出发,双向奔赴。那当然第二种情况下 A 和 B 可以更快相遇。

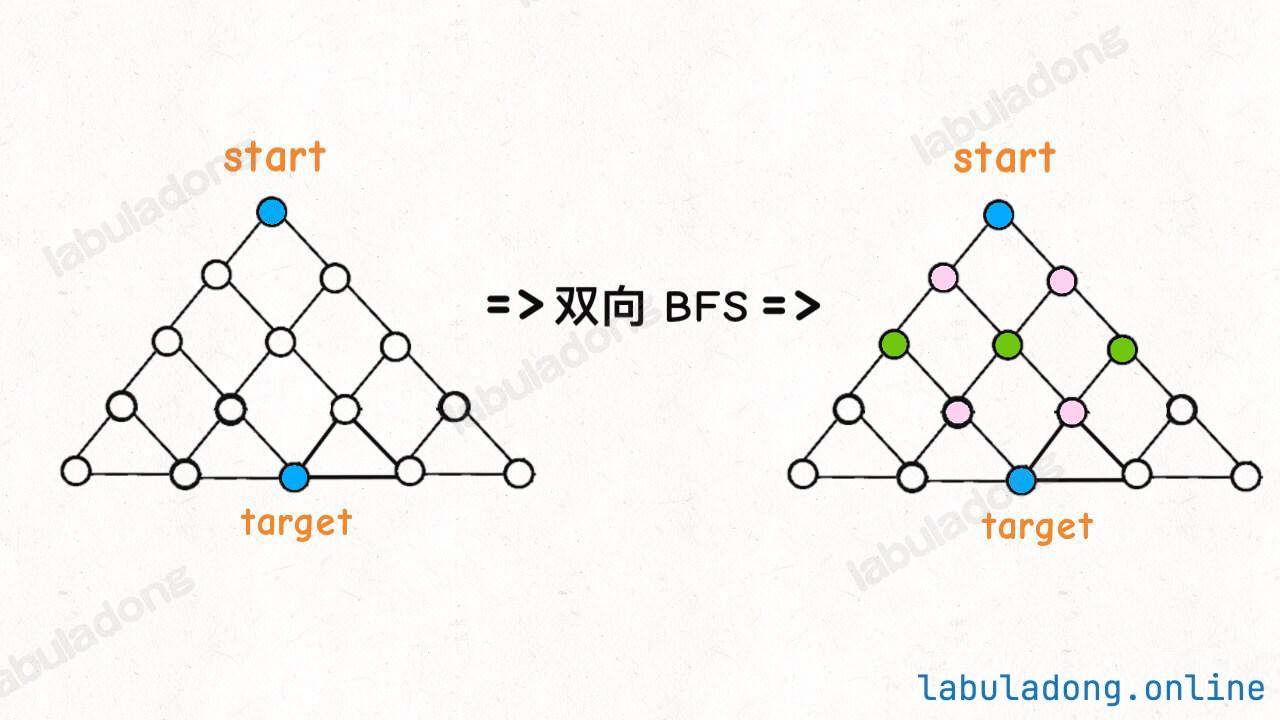
图示中的树形结构,如果终点在最底部,按照传统 BFS 算法的策略,会把整棵树的节点都搜索一遍,最后找到 target;而双向 BFS 其实只遍历了半棵树就出现了交集,也就是找到了最短距离。
当然从 Big O 表示法分析算法复杂度的话,这两种 BFS 在最坏情况下都可能遍历完所有节点,所以理论时间复杂度都是 O(N),但实际运行中双向 BFS 确实会更快一些。
双向 BFS 的局限性
你必须知道终点在哪里,才能使用双向 BFS 进行优化。
对于 BFS 算法,我们肯定是知道起点的,但是终点具体是什么,我们在一开始可能并不知道。
比如上面的密码锁问题和滑动拼图问题,题目都明确给出了终点,都可以用双向 BFS 进行优化。
但比如我们在
二叉树的 DFS/BFS 遍历 中讨论的二叉树最小高度的问题,起点是根节点,终点是距离根节点最近的叶子节点,你在算法开始时并不知道终点具体在哪里,所以就没办法使用双向 BFS 进行优化。
下面我们就以密码锁问题为例,看看如何将普通 BFS 算法优化为双向 BFS 算法,直接看代码吧:
func openLock(deadends []string, target string) int {
deads := make(map[string]struct{})
for _, s := range deadends {
deads[s] = struct{}{}
}
// base case
if _, found := deads["0000"]; found {
return -1
}
if target == "0000" {
return 0
}
// 用集合不用队列,可以快速判断元素是否存在
q1 := make(map[string]struct{})
q2 := make(map[string]struct{})
visited := make(map[string]struct{})
step := 0
q1["0000"] = struct{}{}
visited["0000"] = struct{}{}
q2[target] = struct{}{}
visited[target] = struct{}{}
for len(q1) != 0 && len(q2) != 0 {
// 在这里增加步数
step++
// 哈希集合在遍历的过程中不能修改,所以用 newQ1 存储邻居节点
newQ1 := make(map[string]struct{})
// 获取 q1 中的所有节点的邻居
for cur := range q1 {
// 将一个节点的未遍历相邻节点加入集合
for _, neighbor := range getNeighbors(cur) {
// 判断是否到达终点
if _, found := q2[neighbor]; found {
return step
}
if _, found := visited[neighbor]; !found {
if _, found := deads[neighbor]; !found {
newQ1[neighbor] = struct{}{}
visited[neighbor] = struct{}{}
}
}
}
}
// newQ1 存储着 q1 的邻居节点
q1 = newQ1
// 因为每次 BFS 都是扩散 q1,所以把元素数量少的集合作为 q1
if len(q1) > len(q2) {
q1, q2 = q2, q1
}
}
return -1
}
// 将 s[j] 向上拨动一次
func plusOne(s string, j int) string {
ch := []rune(s)
if ch[j] == '9' {
ch[j] = '0'
} else {
ch[j]++
}
return string(ch)
}
// 将 s[i] 向下拨动一次
func minusOne(s string, j int) string {
ch := []rune(s)
if ch[j] == '0' {
ch[j] = '9'
} else {
ch[j]--
}
return string(ch)
}
func getNeighbors(s string) []string {
neighbors := []string{}
for i := 0; i < 4; i++ {
neighbors = append(neighbors, plusOne(s, i))
neighbors = append(neighbors, minusOne(s, i))
}
return neighbors
}
双向 BFS 还是遵循 BFS 算法框架的,但是有几个细节区别:
1、不再使用队列存储元素,而是改用 哈希集合,方便快速判两个集合是否有交集。
2、调整了 return step 的位置。因为双向 BFS 中不再是简单地判断是否到达终点,而是判断两个集合是否有交集,所以要在计算出邻居节点时就进行判断。
3、还有一个优化点,每次都保持 q1 是元素数量较小的集合,这样可以一定程度减少搜索次数。
因为按照 BFS 的逻辑,队列(集合)中的元素越多,扩散邻居节点之后新的队列(集合)中的元素就越多;在双向 BFS 算法中,如果我们每次都选择一个较小的集合进行扩散,那么占用的空间增长速度就会慢一些,效率就会高一些。
不过话说回来,无论传统 BFS 还是双向 BFS,无论做不做优化,从 Big O 衡量标准来看,时间复杂度都是一样的,只能说双向 BFS 是一种进阶技巧,算法运行的速度会相对快一点,掌握不掌握其实都无所谓。
最关键的还是要把 BFS 通用框架记下来,并且做到熟练运用,后面有 BFS 习题章节,请你尝试运用本文的技巧,解决其中的题目。