回溯算法解题套路框架

这篇文章是很久之前的一篇 回溯算法详解 的进阶版。把框架给你讲清楚，你会发现回溯算法问题都是一个套路。

本文解决几个问题：

回溯算法是什么？解决回溯算法相关的问题有什么技巧？如何学习回溯算法？回溯算法代码是否有规律可循？

其实回溯算法和我们常说的 DFS 算法基本可以认为是同一种算法，它们的细微差异我在 关于 DFS 和回溯算法的若干问题 中有详细解释，本文聚焦回溯算法，不展开。

抽象地说，解决一个回溯问题，实际上就是遍历一棵决策树的过程，树的每个叶子节点存放着一个合法答案。你把整棵树遍历一遍，把叶子节点上的答案都收集起来，就能得到所有的合法答案。

站在回溯树的一个节点上，你只需要思考 3 个问题：

1、路径：也就是已经做出的选择。

2、选择列表：也就是你当前可以做的选择。

3、结束条件：也就是到达决策树底层，无法再做选择的条件。

如果你不理解这三个词语的解释，没关系，我们后面会用「全排列」这个经典的回溯算法问题来帮你理解这些词语是什么意思，现在你先留着印象。

代码方面，回溯算法的框架：

result = []
def backtrack(路径, 选择列表):
    if 满足结束条件:
        result.add(路径)
        return

    for 选择 in 选择列表:
        做选择
        backtrack(路径, 选择列表)
        撤销选择

其核心就是 for 循环里面的递归，在递归调用之前「做选择」，在递归调用之后「撤销选择」，特别简单。

什么叫做选择和撤销选择呢，这个框架的底层原理是什么呢？下面我们就通过「全排列」这个问题来解开之前的疑惑，详细探究一下其中的奥妙！

全排列问题解析

力扣第 46 题「全排列」就是给你输入一个数组 nums，让你返回这些数字的全排列。

我们这次讨论的全排列问题不包含重复的数字，包含重复数字的扩展场景我在后文
回溯算法秒杀排列组合子集的九种题型 中讲解。

另外，有些读者之前看过的全排列算法代码可能是那种 swap 交换元素的写法，和我在本文介绍的代码不同。这是回溯算法两种穷举思路，我会在后文
球盒模型：回溯算法穷举的两种视角 讲明白。现在还不适合直接跟你讲那个解法，你照着我的思路学习即可。

我们在高中的时候就做过排列组合的数学题，我们也知道 n 个不重复的数，全排列共有 n! 个。那么我们当时是怎么穷举全排列的呢？

比方说给三个数 [1,2,3]，你肯定不会无规律地乱穷举，一般是这样：

先固定第一位为 1，然后第二位可以是 2，那么第三位只能是 3；然后可以把第二位变成 3，第三位就只能是 2 了；然后就只能变化第一位，变成 2，然后再穷举后两位……

其实这就是回溯算法，我们高中无师自通就会用，或者有的同学直接画出如下这棵回溯树：

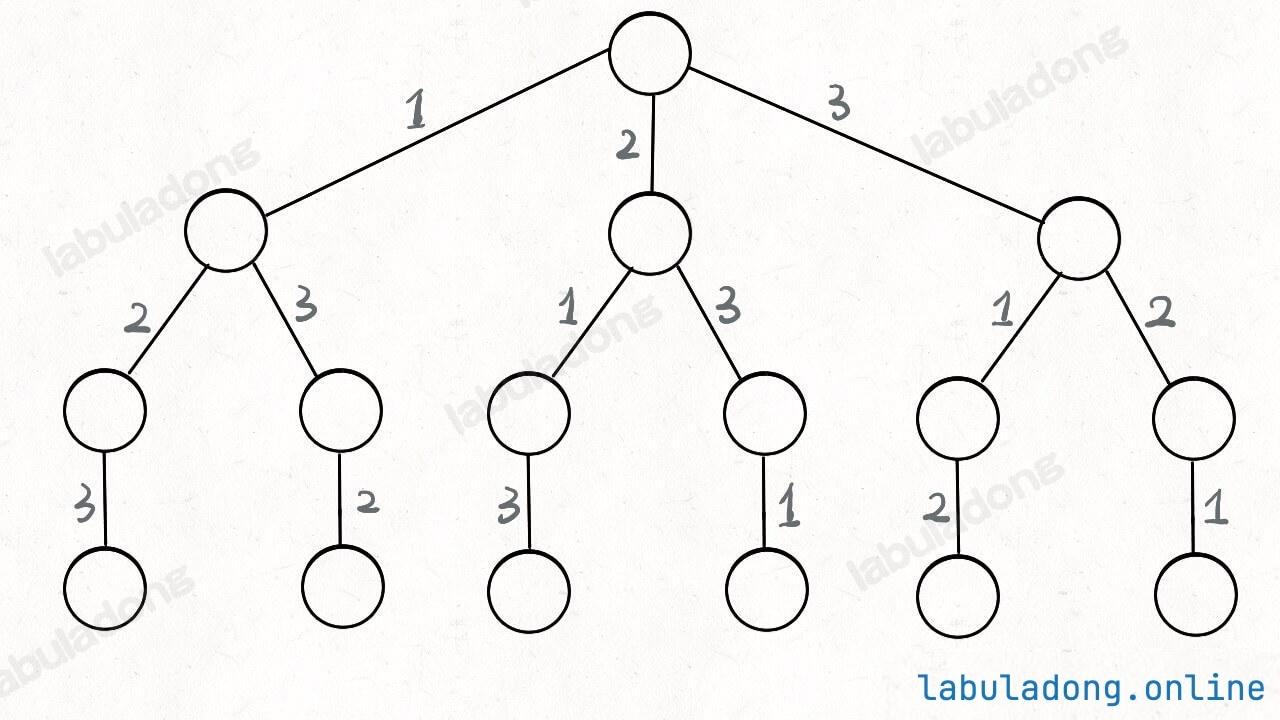
只要从根遍历这棵树，记录路径上的数字，其实就是所有的全排列。我们不妨把这棵树称为回溯算法的「决策树」。

为啥说这是决策树呢，因为你在每个节点上其实都在做决策。比如说你站在下图的红色节点上：

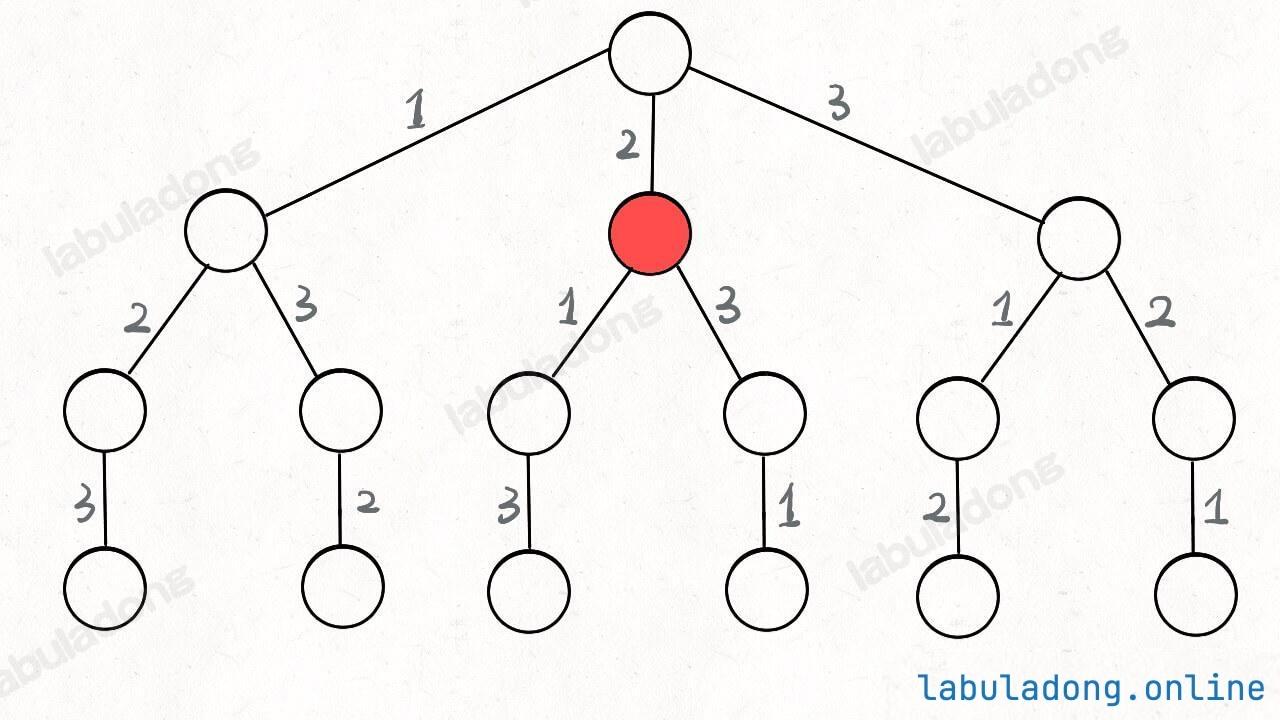
你现在就在做决策，可以选择 1 那条树枝，也可以选择 3 那条树枝。为啥只能在 1 和 3 之中选择呢？因为 2 这个树枝在你身后，这个选择你之前做过了，而全排列是不允许重复使用数字的。

现在可以解答开头的几个名词：[2] 就是「路径」，记录你已经做过的选择；[1,3] 就是「选择列表」，表示你当前可以做出的选择；「结束条件」就是遍历到树的底层叶子节点，这里也就是选择列表为空的时候。

如果明白了这几个名词，可以把「路径」和「选择」列表作为决策树上每个节点的属性，比如下图列出了几个蓝色节点的属性：

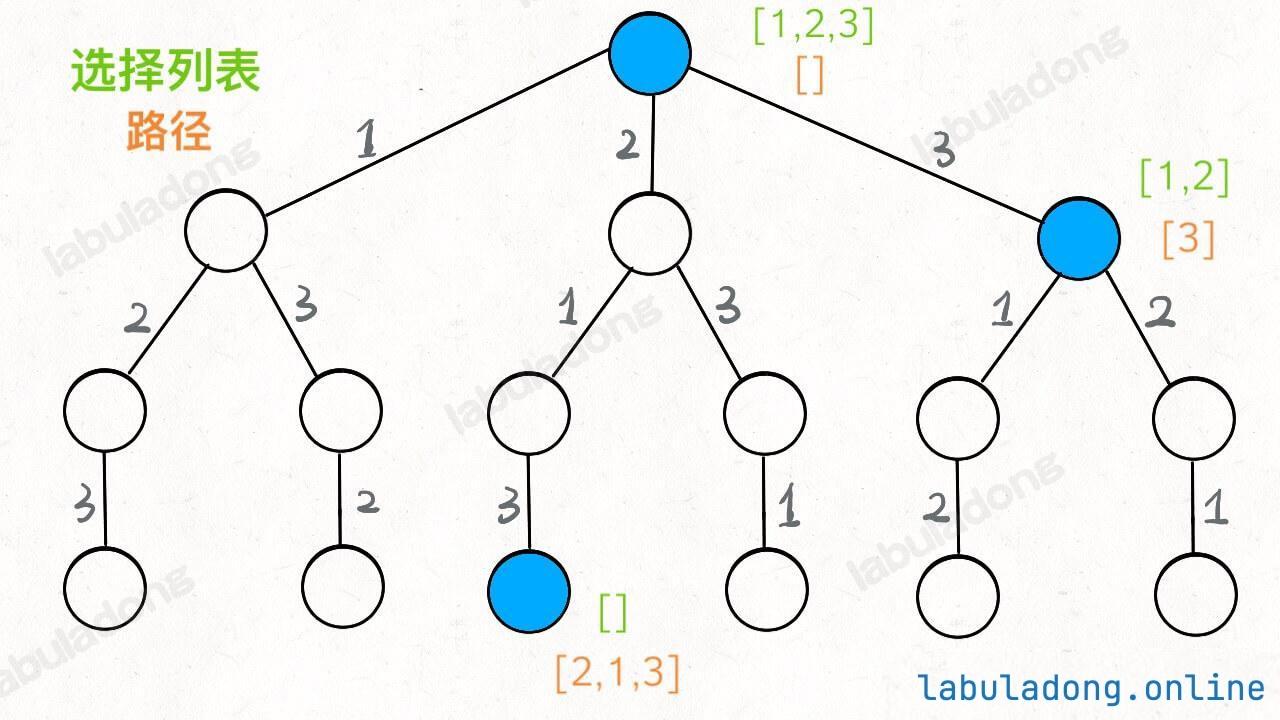
我们定义的 backtrack 函数其实就像一个指针，在这棵树上游走，同时要正确维护每个节点的属性，每当走到树的底层叶子节点，其「路径」就是一个全排列。

再进一步，如何遍历一棵树？这个应该不难吧。回忆一下之前 学习数据结构的框架思维 写过，各种搜索问题其实都是树的遍历问题，而多叉树的遍历框架就是这样：

func traverse(root *TreeNode) {
    for _, child := range root.children {
        // 前序位置需要的操作
        traverse(child)
        // 后序位置需要的操作
    }
}

细心的读者肯定会疑问：多叉树 DFS 遍历框架的前序位置和后序位置应该在 for 循环外面，并不应该是在 for 循环里面呀？为什么在回溯算法中跑到 for 循环里面了？

是的，DFS 算法的前序和后序位置应该在 for 循环外面，不过回溯算法和 DFS 算法略有不同，
解答回溯/DFS 算法的若干疑问 会具体讲解，这里可以暂且忽略这个问题。

而所谓的前序遍历和后序遍历，他们只是两个很有用的时间点，我给你画张图你就明白了：

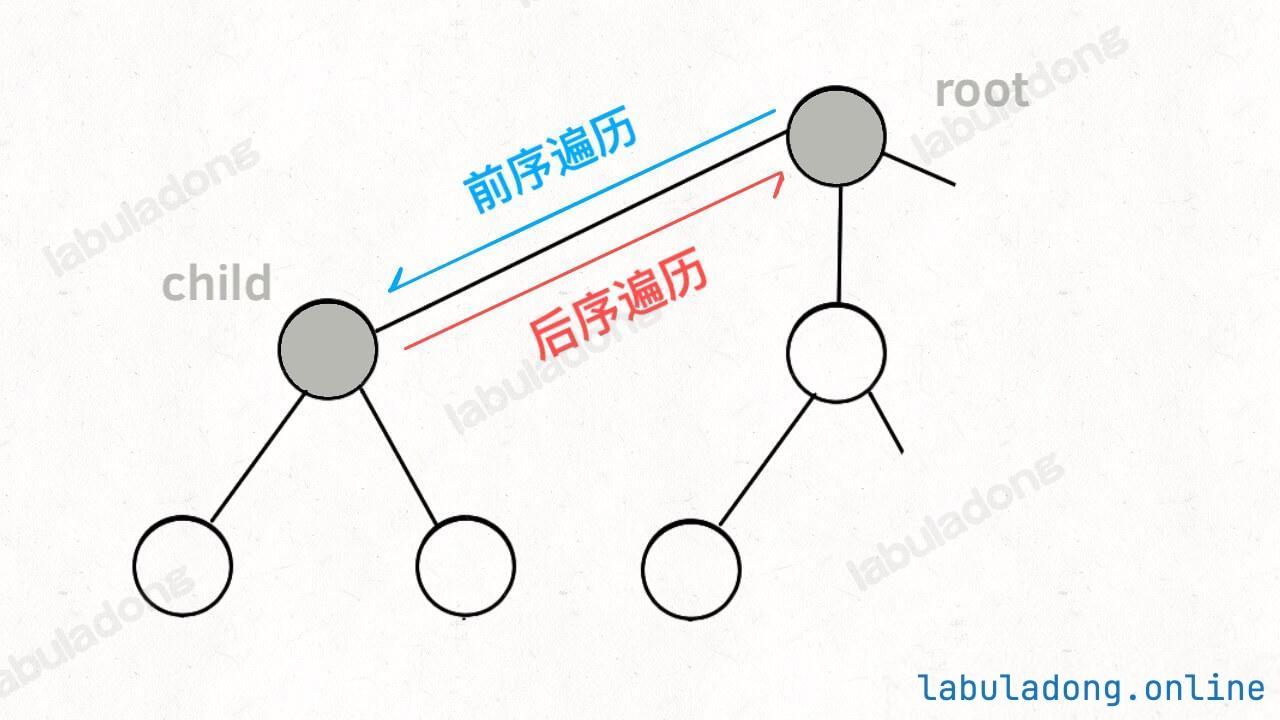
前序遍历的代码在进入某一个节点之前的那个时间点执行，后序遍历代码在离开某个节点之后的那个时间点执行。

回想我们刚才说的，「路径」和「选择」是每个节点的属性，函数在树上游走要正确处理节点的属性，那么就要在这两个特殊时间点搞点动作：

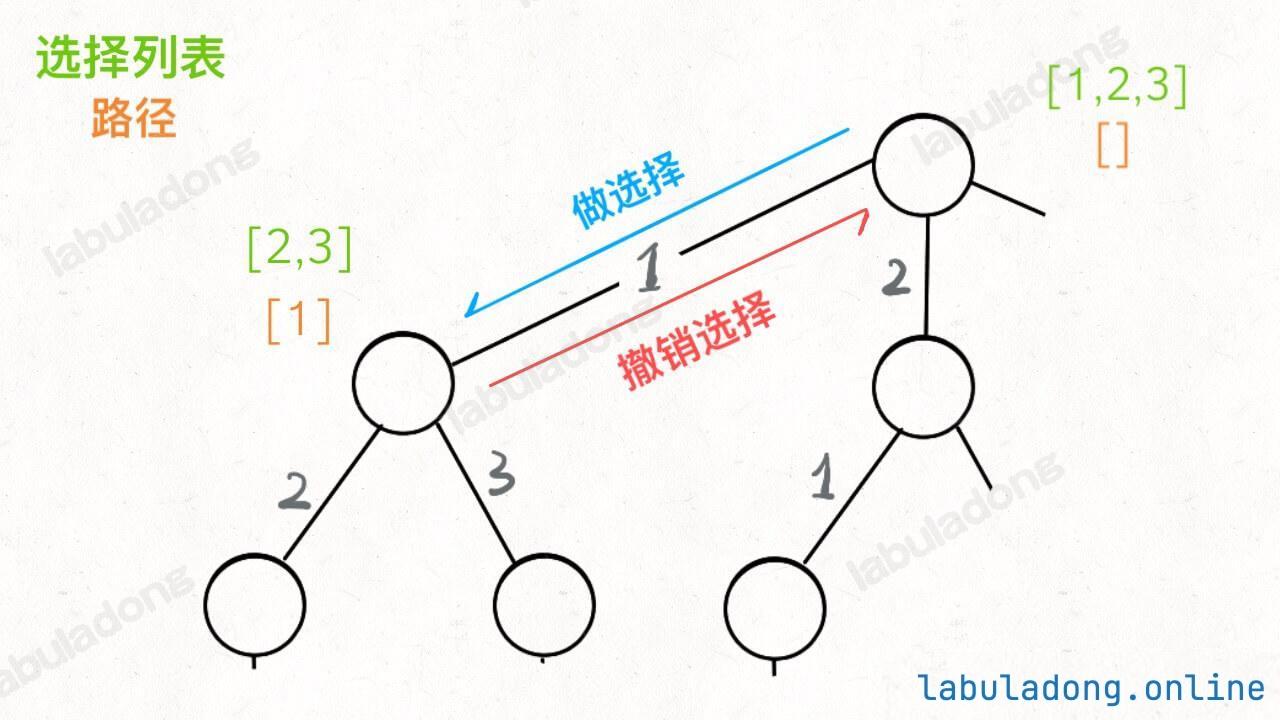
现在，你是否理解了回溯算法的这段核心框架？

for 选择 in 选择列表:
    # 做选择
    将该选择从选择列表移除
    路径.add(选择)
    backtrack(路径, 选择列表)
    # 撤销选择
    路径.remove(选择)
    将该选择再加入选择列表

我们只要在递归之前做出选择，在递归之后撤销刚才的选择，就能正确得到每个节点的选择列表和路径。

下面，直接看全排列代码：

func permute(nums []int) [][]int {
    res := [][]int{}
    // 记录「路径」
    track := []int{}
    // 「路径」中的元素会被标记为 true，避免重复使用
    used := make([]bool, len(nums))

    backtrack(nums, track, used, &res)
    return res
}

// 路径：记录在 track 中
// 选择列表：nums 中不存在于 track 的那些元素（used[i] 为 false）
// 结束条件：nums 中的元素全都在 track 中出现
func backtrack(nums []int, track []int, used []bool, res *[][]int) {
    // 触发结束条件
    if len(track) == len(nums) {
        temp := make([]int, len(track))
        copy(temp, track)
        *res = append(*res, temp)
        return
    }

    for i := 0; i < len(nums); i++ {
        // 排除不合法的选择
        if used[i] {
            // nums[i] 已经在 track 中，跳过
            continue
        }
        // 做选择
        track = append(track, nums[i])
        used[i] = true
        // 进入下一层决策树
        backtrack(nums, track, used, res)
        // 取消选择
        track = track[:len(track)-1]
        used[i] = false
    }
}

我们这里稍微做了些变通，没有显式记录「选择列表」，而是通过 used 数组排除已经存在 track 中的元素，从而推导出当前的选择列表：

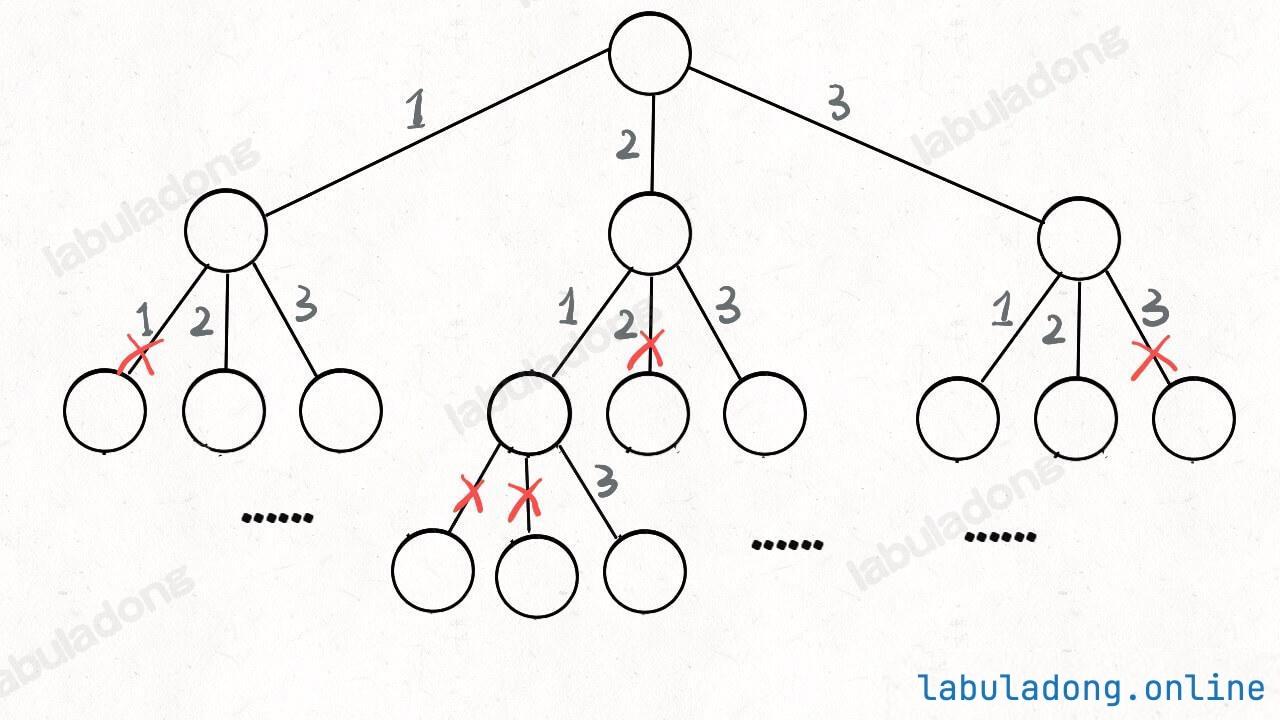
至此，我们就通过全排列问题详解了回溯算法的底层原理。当然，这个算法解决全排列不是最高效的，你可能看到有的解法连 used 数组都不使用，通过交换元素达到目的。但是那种解法稍微难理解一些，我会在 球盒模型：回溯算法两种穷举视角 中介绍。

但是必须说明的是，不管怎么优化，都符合回溯框架，而且时间复杂度都不可能低于 O(N!)，因为穷举整棵决策树是无法避免的，你最后肯定要穷举出 N! 种全排列结果。

这也是回溯算法的一个特点，不像动态规划存在重叠子问题可以优化，回溯算法就是纯暴力穷举，复杂度一般都很高。

最后总结

回溯算法就是个多叉树的遍历问题，关键就是在前序遍历和后序遍历的位置做一些操作，算法框架如下：

def backtrack(...):
    for 选择 in 选择列表:
        做选择
        backtrack(...)
        撤销选择

写 backtrack 函数时，需要维护走过的「路径」和当前可以做的「选择列表」，当触发「结束条件」时，将「路径」记入结果集。

其实想想看，回溯算法和动态规划是不是有点像呢？我们在动态规划系列文章中多次强调，动态规划的三个需要明确的点就是「状态」「选择」和「base case」，是不是就对应着走过的「路径」，当前的「选择列表」和「结束条件」？

动态规划和回溯算法底层都把问题抽象成了树的结构，但这两种算法在思路上是完全不同的。在 二叉树心法（纲领篇） 你将看到动态规划和回溯算法更深层次的区别和联系。