图结构最短路径算法概览

一句话总结

Dijkstra 算法和 A* 算法是 图的 BFS 遍历 的拓展，可以处理不包含负权重的单源最短路径问题。

SPFA 算法（基于队列的 Bellman-Ford 算法）是 图的 BFS 遍历 的拓展，可以处理包含负权重的单源最短路径问题。

Floyd 算法是 动态规划 的应用，可以处理多源最短路径问题。

初学者不要觉得图论算法有多难，因为它们都是基于简单的算法思想扩展出来的。你把基本的二叉树层序遍历玩明白，自己都能发明出来这些算法，没啥了不起的。

考虑到目前处在基础知识章节，所以本文并不会详细讲解每种算法的完整代码，具体的代码实现会安排在之后的章节。

本文的重点在这些算法的关键原理、适用场景，以及这些高级算法和基础知识的联系，帮助初学者对图结构的最短路径算法有一个整体的认识。

最短路径问题概览

最短路径问题在生活中应用广泛，比方说计算最小成本、最短路径长度、最少时间等。

在算法中，我们一般把这类问题抽象成计算 加权图 中的最小路径权重。为了方便表述，在本文中「最短路径」和「最小路径权重和」是等价的。

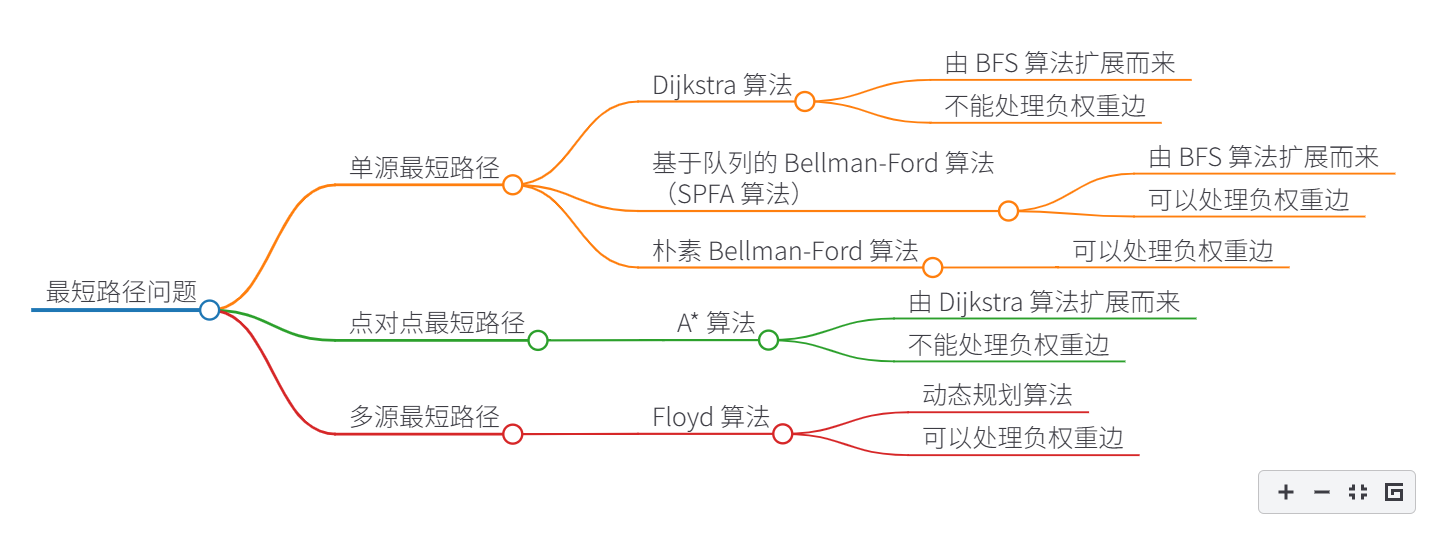
最短路径问题大致可以分为「单源最短路径」和「多源最短路径」两类，下面会介绍几个经典的算法。

单源最短路径

所谓单源最短路径，就是让你计算从某个起点出发，到其他所有顶点的最短路径。

比方说一幅图中有 n 个节点，编号为 0, 1, 2, ..., n-1，让你计算从 2 号节点到其他节点的最短路径，这就是单源最短路径问题。

单源最短路径算法最终得到的输出应该是一个一维数组 distTo，distTo[i] 表示从起点到节点 i 的最短路径长度。

比较有代表性的单源最短路径算法有：

1、Dijkstra 算法，其本质是 BFS 算法 + 贪心思想，效率较高，但是不能处理带有负权重的图。

2、基于队列的 Bellman-Ford 算法，其本质也是 BFS 算法，可以处理带有负权重的图，但效率比 Dijkstra 算法低。

点对点最短路径

很多算法题中不需要我们计算起点到所有其他节点的最短路径，仅需要计算从起点 src 到某一个目标节点 dst 的最短路径。这类问题可以称为点对点最短路径问题。

一般来说，点对点最短路径问题可以视为单源最短路径问题的特例，你可以从 src 开始执行单源最短路径算法，当算出到达 dst 的最短路径时提前结束算法。

但是下面将介绍一种专门处理点对点问题的算法：A* 算法（A Star Algorithm）。

我经常讲，算法的本质是穷举，你想要提高穷举的效率，就得尽可能充分地利用信息。点对点最短路径问题（已知起点和终点）比单源最短路径问题（已知起点）多了终点信息，所以完全有可能利用这个信息来提高算法的效率。

比方说，如果我们知道终点在起点的右下方，那么我们有理由猜测：应该优先向右下方搜索，可能可以更快地到达终点。

A* 算法的关键就在这里：它能够充分利用已知信息，有方向性地进行搜索，更快地找到终点。我们称这类算法为启发式搜索算法（Heuristic Search Algorithm）。

但是请注意，这个猜测只是经验法则，并不一定总是正确。比方说右下方可能都是死路，偏偏就得经过左上角绕个大弯才能到达终点。

所以启发式算法需要合理设置启发函数（Heuristic Function），在经验法则和实际情况中找到平衡，确保在经验法则失效时，算法的效率也不会太差。

多源最短路径

所谓多源最短路径，就是让你计算任意两节点之间的最短路径。

比方说一幅图中有 n 个节点，编号为 0, 1, 2, ..., n-1，让你计算所有节点之间的最短路径，这就是多源最短路径问题。

多源最短路径算法最终得到的输出应该是一个二维数组 dist，dist[i][j] 表示从节点 i 到节点 j 的最短路径长度。

最有代表性的是 Floyd 算法，其本质是动态规划算法。

理论上，我们对所有节点都调用一次单源最短路径算法，就可以得到多源最短路径的解。

但具体实现时，要根据图结构的特点来选择。有些场景用 Floyd 这种多源最短路径算法效率更高，有些场景多次调用 Dijkstra 这种单源最短路径算法效率更高。后面讲到这些算法的复杂度时，你就能理解了。

负权重边的影响

在计算最短路径时，需要着重注意的是这幅图是否包含负权重边；一旦包含负权重边，一定要检查是否包含负权重环。

为啥负权重边会影响最短路径算法呢？因为负权重边会让问题变得复杂。举个最简单的例子就能直观地理解了：

比方说我们现在站在起点 s 上，相邻节点有 a 和 b，s->a 权重为 3，s->b 权重为 4。

如果这幅图不存在负权重边，那么根据上述信息，我就已经可以确定 s 到 a 的最短路径是 s->a，权重和为 3。因为你从 s->b 这条路径走出去，绕一圈到达 a 的路径权重和肯定是大于 4 的，不可能比 3 还小。

但如果这幅图存在负权重边，那可就不一定了。因为可能出现负权重边呀，比方说 b->a 的权重为 -10，那么从 s->b->a 的路径权重和为 -6，比 s->a 的路径权重和 3 还小。

想让 Dijkstra 这类包含贪心思想的算法成立，需要一个前提：它假设随着经过的边的数量增加，路径权重和一定也会增加。但负权重边的出现打破了这一假设，导致算法失效。

如果图中存在负权重环，最短路径问题就没有意义了。比方说 s 到 a 的路径上存在负权重环，那么你可以在这个负权重环上无限转圈，使得路径权重和无限减小下去。

常见最短路径算法中，Dijkstra 算法和 A* 算法不能处理含有负权重边的图，Floyd 算法和 Bellman-Ford 算法可以处理负权重边，Bellman-Ford 算法常用来检测负权重环。

下面，我们介绍这些算法的核心原理。

Dijkstra 算法简介

Dijkstra 算法的本质就是 BFS 算法 + 贪心思路，可以解决不包含负权重的单源最短路径问题。

其实你可以很容易地直接从标准的 BFS 遍历出发，推演出 Dijkstra 算法的代码。来思考标准的 二叉树 BFS（层序）遍历 和 图的 BFS 遍历，为什么它们能算出最短路径？

因为它们的场景中都是无权边，可以认为每条边的权重都是 1，所以边的条数就等同于路径的权重和；由于 BFS 逐层扩散的逻辑，最先到达终点的路径经过的边数就是最少的，也就是路径权重和最小的路径。

现在考虑加权图，其中每条边可能有不同的权重，边最少的路径，不一定是权重和最小的，所以路径中边的条数已经没有意义了。

首先，我们需要用到 图的 BFS 遍历 中第三种代码实现，让 BFS 算法关注路径的权重和而不是边的数量。

另外，我们需要优先扩散权重和最小的路径，最先到达终点的路径就是权重和最小的路径。这就是贪心思想的体现，在讲代码实现时我们会进行数学证明。

如何优先扩散权重和最小的路径呢？借助 优先级队列 把权重小的路径排前面，优先级队列的逻辑是每次出队权重最小的节点，最先到达终点的路径就是权重和最小的路径。

对比标准 BFS 算法，只需修改两个地方即可得到 Dijkstra 算法：

1、标准 BFS 算法使用普通队列，Dijkstra 算法使用优先级队列。

2、标准 BFS 算法使用一个 visited 数组记录访问过的节点，确保算法不会陷入死循环；Dijkstra 算法使用一个 distTo 数组，确保算法不会陷入死循环，同时记录起点到其他节点的最短路径。

对于初学者来说，上面的描述可能有点抽象，不过不用担心，你现在只需要知道 Dijkstra 算法就是 BFS 算法的变种就行了。具体的代码实现和例题参见 Dijkstra 算法详解。

A* 算法简介

对于任意节点 x，我们用 g(x) 表示从起点 src 到节点 x 的距离，用 h(x) 表示启发函数，用于估计从节点 x 到终点 dst 的距离。那么 Dijkstra 算法就是借助优先级队列，让 g(x) 最小的节点先出队，从而保证终点第一次出队时，就找到了最短路径。

而 A* 算法中稍作了一点改动：让 f(x)=g(x)+h(x) 最小的节点优先出队，终点第一次出队时，就找到了最短路径。

仔细想想，f(x) 函数虽然简单，却非常精妙：

无论是接近终点还是远离终点，g(x) 肯定是不断增大的。 但是接近终点时，h(x) 会逐渐减小；远离终点时，h(x) 会逐渐增大。 也就是说，接近终点时 f(x) 会变小，节点更容易出队，算法也就会优先向终点的方向进行搜索；反之，远离终点时 f(x) 会变大，搜索的优先级就会降低。

只需要稍微修改 Dijkstra 算法的代码即可得到 A* 算法的代码，具体实现及应用场景会在后面的章节介绍。

Bellman-Ford/SPFA 算法简介

当说到包含负权重边的最短路径问题是，经常提到 Bellman-Ford 算法和 SPFA 算法（Shortest Path Faster Algorithm）。

这里有必要先澄清一下：当我们说 Bellman-Ford 算法时，一般是指 朴素 Bellman-Ford 算法；当我们说 SPFA 算法时，是指对朴素 Bellman-Ford 算法的一种优化，即 基于队列的 Bellman-Ford 算法。

这里仅介绍 SPFA 算法，因为可以通过标准 BFS 算法推导出来。朴素 Bellman-Ford 算法会在讲解代码实现时再介绍。

对比标准的 BFS 算法，SPFA 算法只有一个地方不一样：

标准 BFS 算法使用一个布尔数组 visited 确保每个节点只会遍历一次，避免算法陷入死循环；SPFA 算法中，需要使用 inQueue, count 数组配合，确保算法不会陷入死循环，同时用一个 distTo 数组记录起点到其他节点的最短路径。

对于初学者来说，上面的描述可能也有点抽象。不过不用担心，你现在只需要知道 SPFA 算法就是 BFS 算法的变种就行了。具体的代码实现和例题会更新在数据结构设计章节。

Floyd 算法简介

Floyd 算法是求解多源最短路径问题的经典算法，它的核心思想是 动态规划，和前面讲的基于 BFS 算法的单源最短路径算法完全不同。

在这个章节肯定没办法给初学者彻底讲清楚 Floyd 算法的原理，只能尽量描述一下这个算法的思路。

假设图中节点 i 和节点 j 之间存在最短路径，应该如何计算节点 i 到节点 j 的最短路径呢？

如果节点 i 和节点 j 之间有直接相连的边，那么节点 i 到节点 j 的最短路径就是这条边的权重。

如果节点 i 和节点 j 之间没有直接相连的边，那么肯定要经过至少 1 个其他节点。

对于任意一个其他节点 k，如果最短路径经过 k，那么节点 i 到节点 j 的最短路径就是节点 i 到节点 k 的最短路径加上节点 k 到节点 j 的最短路径。

这样一来，原问题「i 到 j 的最短路径」就变成了两个结构相同，规模更小的子问题「i 到 k 的最短路径」和「k 到 j 的最短路径」，这就是动态规划的特征，我们将根据这个思路来推导转移方程。

是不是对上面的描述有些懵圈？不必担心，虽然 Floyd 算法的核心代码只有 3 行，但状态转移方程确实不容易理解， Floyd 算法原理及应用 中会详细讲解。