图结构的通用代码实现

一句话总结

图结构就是多叉树结构的延伸。图结构逻辑上由若干节点（Vertex）和边（Edge）构成，我们一般用邻接表、邻接矩阵等方式来存储图。

在树结构中，只允许父节点指向子节点，不存在子节点指向父节点的情况，子节点之间也不会互相链接；而图中没有那么多限制，节点之间可以相互指向，形成复杂的网络结构。

图结构可以对很多复杂的问题进行抽象，产生了很多经典的图论算法，比如二分图算法、拓扑排序、最短路径算法、最小生成树算法等，这些都会在后文介绍。

本文主要介绍图的基本概念，以及如何用代码实现图结构。

图的逻辑结构

一幅图是由节点 (Vertex) 和边 (Edge) 构成的，逻辑结构如下：

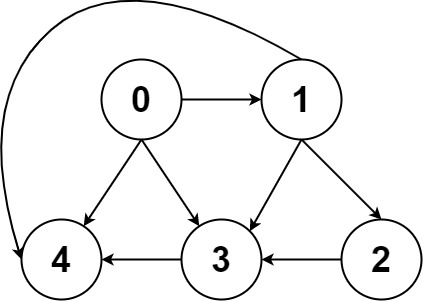
tuluojijiegou

注意看我把「逻辑结构」和「具体实现」分开了。就好比前文二叉堆的原理和实现一样，二叉堆的逻辑结构是一棵完全二叉树，但我们实际上用的数组来实现它。

根据图的逻辑结构，我们可以认为每个节点的实现如下：

// 图节点的逻辑结构
type Vertex struct {
    id        int
    neighbors []*Vertex
}

看到这个实现，你有没有很熟悉？它和我们之前说的多叉树节点几乎完全一样：

// 基本的 N 叉树节点
type TreeNode struct {
    val      int
    children []*TreeNode
}

所以说，图真的没啥高深的，本质上就是个高级点的多叉树而已，适用于树的 DFS/BFS 遍历算法，全部适用于图。

上面讲解的图结构是「逻辑上的」，具体实现上，我们很少用这个 Vertex 类，而是用邻接表、邻接矩阵来实现图结构。

邻接表和邻接矩阵实现图结构

邻接表和邻接矩阵是图结构的两种实现方法。

比如还是这幅图：

tuluojijiegou

用邻接表和邻接矩阵的存储方式分别如下：

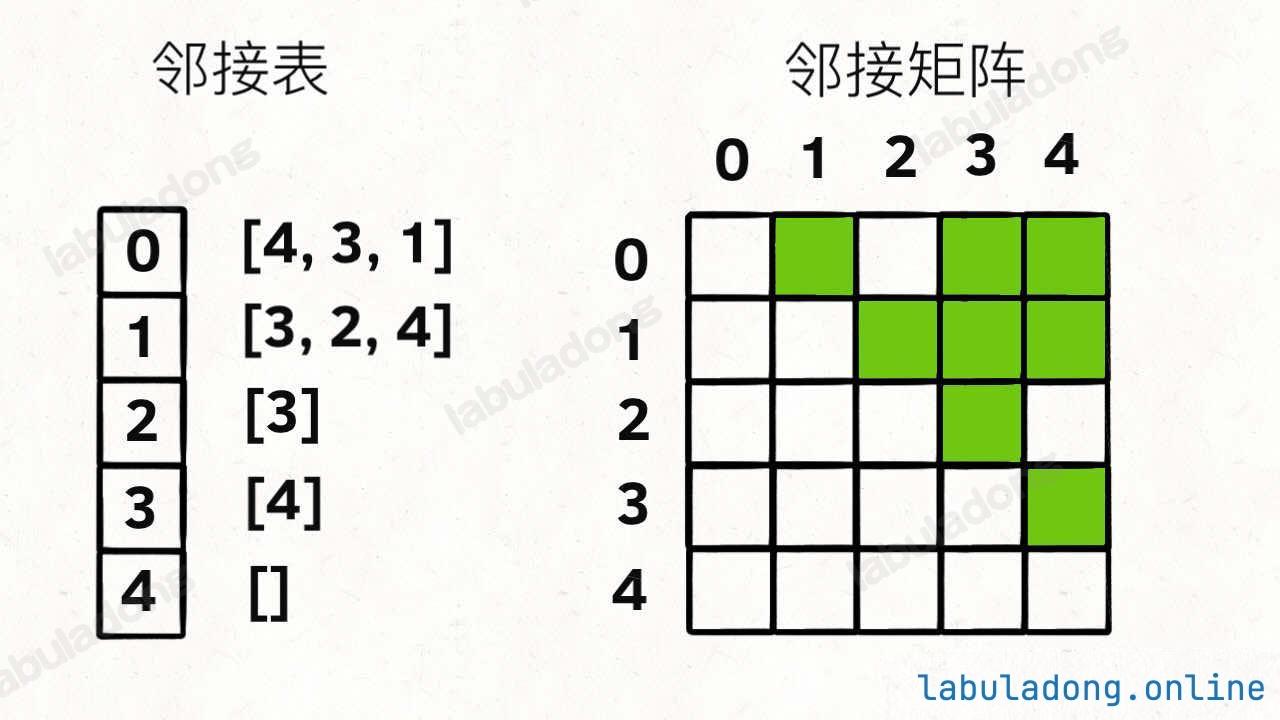
lingjiejuzheng

邻接表很直观，我把每个节点 x 的邻居都存到一个列表里，然后把 x 和这个列表映射起来，这样就可以通过一个节点 x 找到它的所有相邻节点。

邻接矩阵则是一个二维布尔数组，我们权且称为 matrix，如果节点 x 和 y 是相连的，那么就把 matrix[x][y] 设为 true（上图中绿色的方格代表 true）。如果想找节点 x 的邻居，去扫一圈 matrix[x][..] 就行了。

如果用代码的形式来表现，邻接表和邻接矩阵大概长这样：

// 邻接表
// graph[x] 存储 x 的所有邻居节点
var graph [][]int

// 邻接矩阵
// matrix[x][y] 记录 x 是否有一条指向 y 的边
var matrix [][]bool

节点类型不是 int 怎么办

上述讲解中，我默认图节点是一个从 0 开始的整数，所以才能存储到邻接表和邻接矩阵中，通过索引访问。

但实际问题中，图节点可能是其他类型，比如字符串、自定义类等，那应该怎么存储呢？

很简单，你再额外使用一个哈希表，把实际节点和整数 id 映射起来，然后就可以用邻接表和邻接矩阵存储整数 id 了。

后面的讲解及习题中，我都会默认图节点是整数 id。

那么，为什么有这两种存储图的方式呢？肯定是因为他们有不同的适用场景。

注意分析两种存储方式的空间复杂度，对于一幅有 V 个节点，E 条边的图，邻接表的空间复杂度是 O(V+E)，而邻接矩阵的空间复杂度是 O(V²)。

所以如果一幅图的 E 远小于 V^2（稀疏图），那么邻接表会比邻接矩阵节省空间，反之，如果 E 接近 V^2（稠密图），二者就差不多了。

在后面的图算法和习题中，大多都是稀疏图，所以你会看到邻接表的使用更多一些。

邻接矩阵的最大优势在于，矩阵是一个强有力的数学工具，图的一些隐晦性质可以借助精妙的矩阵运算展现出来。不过本文不准备引入数学内容，所以有兴趣的读者可以自行搜索学习。

这也是为什么一定要把图节点类型转换成整数 id 的原因，不然的话你怎么用矩阵运算呢？

不同种类的图结构

那你可能会问，我们上面说的这个图的模型仅仅是「有向无权图」，不是还有什么加权图，无向图，等等……

其实，这些更复杂的模型都是基于这个最简单的图衍生出来的。

有向加权图怎么实现？很简单呀：

如果是邻接表，我们不仅仅存储某个节点 x 的所有邻居节点，还存储 x 到每个邻居的权重，不就实现加权有向图了吗？

如果是邻接矩阵，matrix[x][y] 不再是布尔值，而是一个 int 值，0 表示没有连接，其他值表示权重，不就变成加权有向图了吗？

如果用代码的形式来表现，大概长这样：

// 邻接表
// graph[x] 存储 x 的所有邻居节点以及对应的权重
// 具体实现不一定非得这样，可以参考后面的通用实现
type Edge struct {
    to     int
    weight int
}
var graph [][]Edge

// 邻接矩阵
// matrix[x][y] 记录 x 指向 y 的边的权重，0 表示不相邻
var matrix [][]int

无向图怎么实现？也很简单，所谓的「无向」，是不是等同于「双向」？

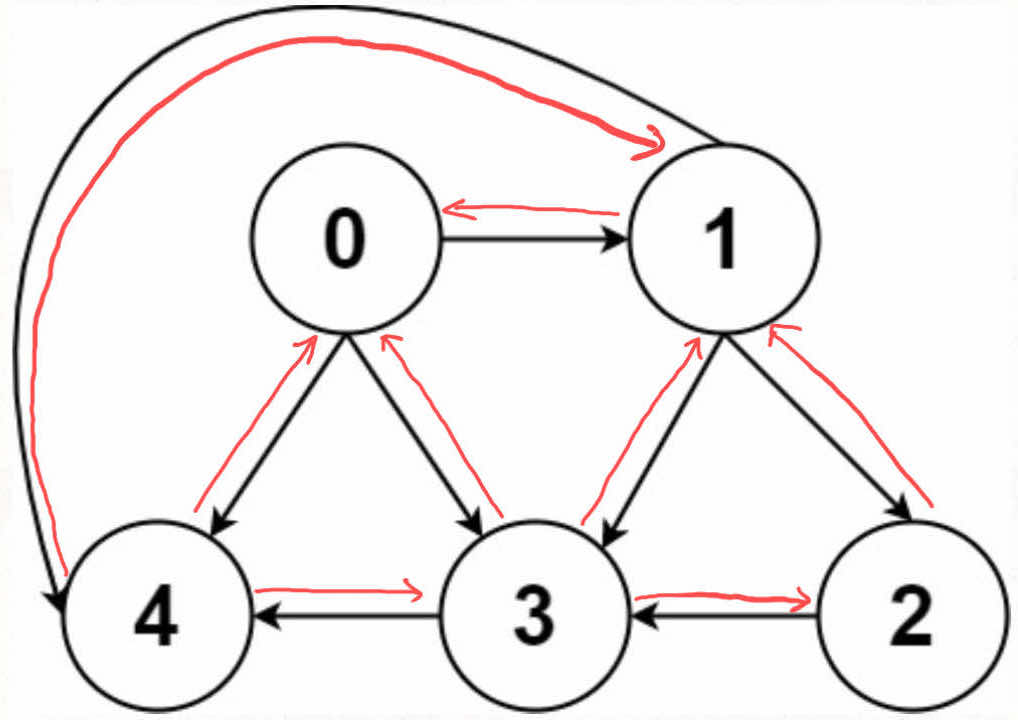
shuangxiangjiaqiantu

如果连接无向图中的节点 x 和 y，把 matrix[x][y] 和 matrix[y][x] 都变成 true 不就行了；邻接表也是类似的操作，在 x 的邻居列表里添加 y，同时在 y 的邻居列表里添加 x。

把上面的技巧合起来，就变成了无向加权图……

好了，关于图的基本介绍就到这里，现在不管来什么乱七八糟的图，你心里应该都有底了。

下面我写一个通用的类，来实现图的基本操作（增删查改）。

图结构的通用代码实现

基于上面的讲解，我们可以抽象出一个 Graph 接口，来实现图的基本增删查改：

type Graph interface {
    // 添加一条边（带权重）
    AddEdge(from int, to int, weight int)

    // 删除一条边
    RemoveEdge(from int, to int)

    // 判断两个节点是否相邻
    HasEdge(from int, to int) bool

    // 返回一条边的权重
    Weight(from int, to int) int

    // 返回某个节点的所有邻居节点和对应权重
    Neighbors(v int) []Edge

    // 返回节点总数
    Size() int
}

这其实是有向加权图的接口，但基于这个接口可以实现所有不同种类的无向/有向/无权/加权图。下面给出具体代码。

有向加权图（邻接表实现）

我这里给出一个简单的通用实现，后文图论算法教程和习题中可能会用到。其中有一些可以优化的点我写在注释中了。

注意

简单起见，下面给出的代码默认输入的都是合法的，不会出现不合法的节点 id，也不会输入重复的边。

在实际的题目中，我们一般也会先剔除掉不合法的数据，然后再进行建图。

import (
    "fmt"
)

// 加权有向图的通用实现（邻接表）
type WeightedDigraph struct {
    graph [][]Edge
}

// 存储相邻节点及边的权重
type Edge struct {
    to     int
    weight int
}

func NewWeightedDigraph(n int) *WeightedDigraph {
    // 我们这里简单起见，建图时要传入节点总数，这其实可以优化
    // 比如把 graph 设置为 map[int][]Edge，就可以动态添加新节点了
    graph := make([][]Edge, n)
    return &WeightedDigraph{graph: graph}
}

// 增，添加一条带权重的有向边，复杂度 O(1)
func (g *WeightedDigraph) AddEdge(from, to, weight int) {
    g.graph[from] = append(g.graph[from], Edge{to: to, weight: weight})
}

// 删，删除一条有向边，复杂度 O(V)
func (g *WeightedDigraph) RemoveEdge(from, to int) {
    for i, e := range g.graph[from] {
        if e.to == to {
            g.graph[from] = append(g.graph[from][:i], g.graph[from][i+1:]...)
            break
        }
    }
}

// 查，判断两个节点是否相邻，复杂度 O(V)
func (g *WeightedDigraph) HasEdge(from, to int) bool {
    for _, e := range g.graph[from] {
        if e.to == to {
            return true
        }
    }
    return false
}

// 查，返回一条边的权重，复杂度 O(V)
func (g *WeightedDigraph) Weight(from, to int) int {
    for _, e := range g.graph[from] {
        if e.to == to {
            return e.weight
        }
    }
    panic("No such edge")
}

// 上面的 HasEdge、RemoveEdge、Weight 方法遍历 List 的行为是可以优化的
// 比如用 map[int]map[int]int 存储邻接表
// 这样就可以避免遍历 List，复杂度就能降到 O(1)

// 查，返回某个节点的所有邻居节点，复杂度 O(1)
func (g *WeightedDigraph) Neighbors(v int) []Edge {
    return g.graph[v]
}

func main() {
    graph := NewWeightedDigraph(3)
    graph.AddEdge(0, 1, 1)
    graph.AddEdge(1, 2, 2)
    graph.AddEdge(2, 0, 3)
    graph.AddEdge(2, 1, 4)

    fmt.Println(graph.HasEdge(0, 1)) // true
    fmt.Println(graph.HasEdge(1, 0)) // false

    for _, edge := range graph.Neighbors(2) {
        fmt.Printf("%d -> %d, weight: %d\n", 2, edge.to, edge.weight)
    }
    // 2 -> 0, weight: 3
    // 2 -> 1, weight: 4

    graph.RemoveEdge(0, 1)
    fmt.Println(graph.HasEdge(0, 1)) // false
}

有向加权图（邻接矩阵实现）

具体请看代码和注释：

// 加权有向图的通用实现（邻接矩阵）
type Edge struct {
    To     int
    Weight int
}

type WeightedDigraph struct {
    // 邻接矩阵，matrix[from][to] 存储从节点 from 到节点 to 的边的权重
    // 0 表示没有连接
    matrix [][]int
}

func NewWeightedDigraph(n int) *WeightedDigraph {
    matrix := make([][]int, n)
    for i := range matrix {
        matrix[i] = make([]int, n)
    }
    return &WeightedDigraph{matrix}
}

// 增，添加一条带权重的有向边，复杂度 O(1)
func (g *WeightedDigraph) AddEdge(from, to, weight int) {
    g.matrix[from][to] = weight
}

// 删，删除一条有向边，复杂度 O(1)
func (g *WeightedDigraph) RemoveEdge(from, to int) {
    g.matrix[from][to] = 0
}

// 查，判断两个节点是否相邻，复杂度 O(1)
func (g *WeightedDigraph) HasEdge(from, to int) bool {
    return g.matrix[from][to] != 0
}

// 查，返回一条边的权重，复杂度 O(1)
func (g *WeightedDigraph) Weight(from, to int) int {
    return g.matrix[from][to]
}

// 查，返回某个节点的所有邻居节点，复杂度 O(V)
func (g *WeightedDigraph) Neighbors(v int) []Edge {
    res := []Edge{}
    for i := 0; i < len(g.matrix[v]); i++ {
        if g.matrix[v][i] > 0 {
            res = append(res, Edge{To: i, Weight: g.matrix[v][i]})
        }
    }
    return res
}

func main() {
    graph := NewWeightedDigraph(3)
    graph.AddEdge(0, 1, 1)
    graph.AddEdge(1, 2, 2)
    graph.AddEdge(2, 0, 3)
    graph.AddEdge(2, 1, 4)

    fmt.Println(graph.HasEdge(0, 1)) // true
    fmt.Println(graph.HasEdge(1, 0)) // false

    for _, edge := range graph.Neighbors(2) {
        fmt.Printf("%d -> %d, weight: %d\n", 2, edge.To, edge.Weight)
    }
    // 2 -> 0, weight: 3
    // 2 -> 1, weight: 4

    graph.RemoveEdge(0, 1)
    fmt.Println(graph.HasEdge(0, 1)) // false
}

有向无权图（邻接表/邻接矩阵实现）

直接复用上面的 WeightedDigraph 类就行，把 addEdge 方法的权重参数默认设置为 1 就行了。比较简单，我就不写代码了。

无向加权图（邻接表/邻接矩阵实现）

无向加权图就等同于双向的有向加权图，所以直接复用上面用邻接表/领接矩阵实现的 WeightedDigraph 类就行了，只是在增加边的时候，要同时添加两条边：

import "fmt"

type WeightedUndigraph struct {
	graph *WeightedDigraph
}

// 新建一个带权重的无向图，传入节点数量
func NewWeightedUndigraph(n int) *WeightedUndigraph {
	return &WeightedUndigraph{graph: NewWeightedDigraph(n)}
}

// 增，添加一条带权重的无向边
func (wg *WeightedUndigraph) addEdge(from, to, weight int) {
	wg.graph.addEdge(from, to, weight)
	wg.graph.addEdge(to, from, weight)
}

// 删，删除一条无向边
func (wg *WeightedUndigraph) removeEdge(from, to int) {
	wg.graph.removeEdge(from, to)
	wg.graph.removeEdge(to, from)
}

// 查，判断两个节点是否相邻
func (wg *WeightedUndigraph) hasEdge(from, to int) bool {
	return wg.graph.hasEdge(from, to)
}

// 查，返回一条边的权重
func (wg *WeightedUndigraph) weight(from, to int) int {
	return wg.graph.weight(from, to)
}

// 查，返回某个节点的所有邻居节点
func (wg *WeightedUndigraph) neighbors(v int) []*Edge {
	return wg.graph.neighbors(v)
}

func main() {
	graph := NewWeightedUndigraph(3)
	graph.addEdge(0, 1, 1)
	graph.addEdge(2, 0, 3)
	graph.addEdge(2, 1, 4)

	fmt.Println(graph.hasEdge(0, 1)) // true
	fmt.Println(graph.hasEdge(1, 0)) // true

	for _, edge := range graph.neighbors(2) {
		fmt.Printf("2 <-> %d, wight: %d\n", edge.to, edge.weight)
	}
	// 2 <-> 0, wight: 3
	// 2 <-> 1, wight: 4

	graph.removeEdge(0, 1)
	fmt.Println(graph.hasEdge(0, 1)) // false
	fmt.Println(graph.hasEdge(1, 0)) // false
}

无向无权图（邻接表/邻接矩阵实现）

直接复用上面的 WeightedUndigraph 类就行，把 addEdge 方法的权重参数默认设置为 1 就行了。比较简单，我就不写代码了。