图论中的基本术语
一幅图结构由若干 节点(Vertex) 和 边 (Edge) 构成,其中:
每个节点有一个唯一 ID。 边可以是有向的(有向图,Directional Graph),也可以是无向的(无向图,Undirected Graph)。 边上可以有权重(加权图,Weighted Graph),也可以没有权重(无权图,Unweighted Graph)。
边的权重和方向
下图是一个有向无权图:
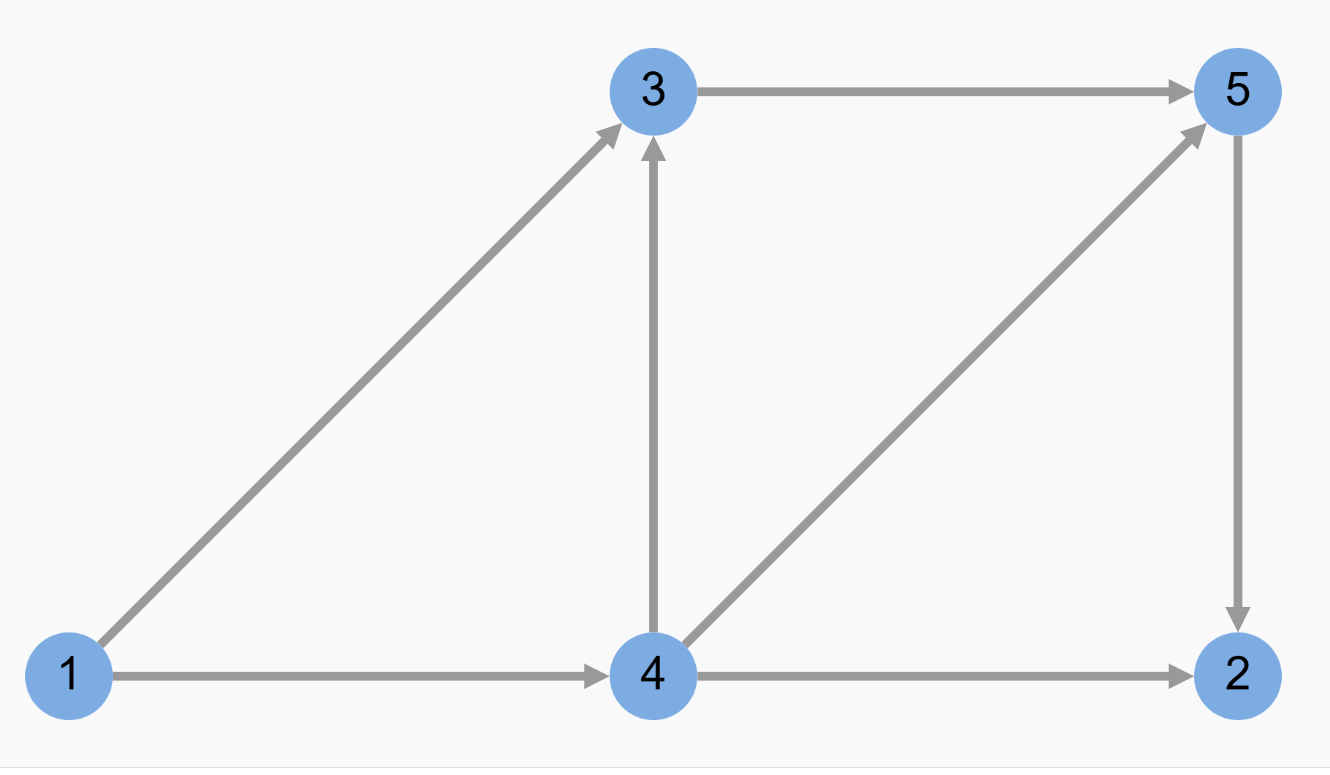
图中有一条从节点 1 指向节点 3 的有向边,这说明可以从节点 1 直接到达节点 3;但由于没有从节点 3 指向节点 1 的有向边,所以节点 3 不能直接到达节点 1。
下图是一个无向无权图:
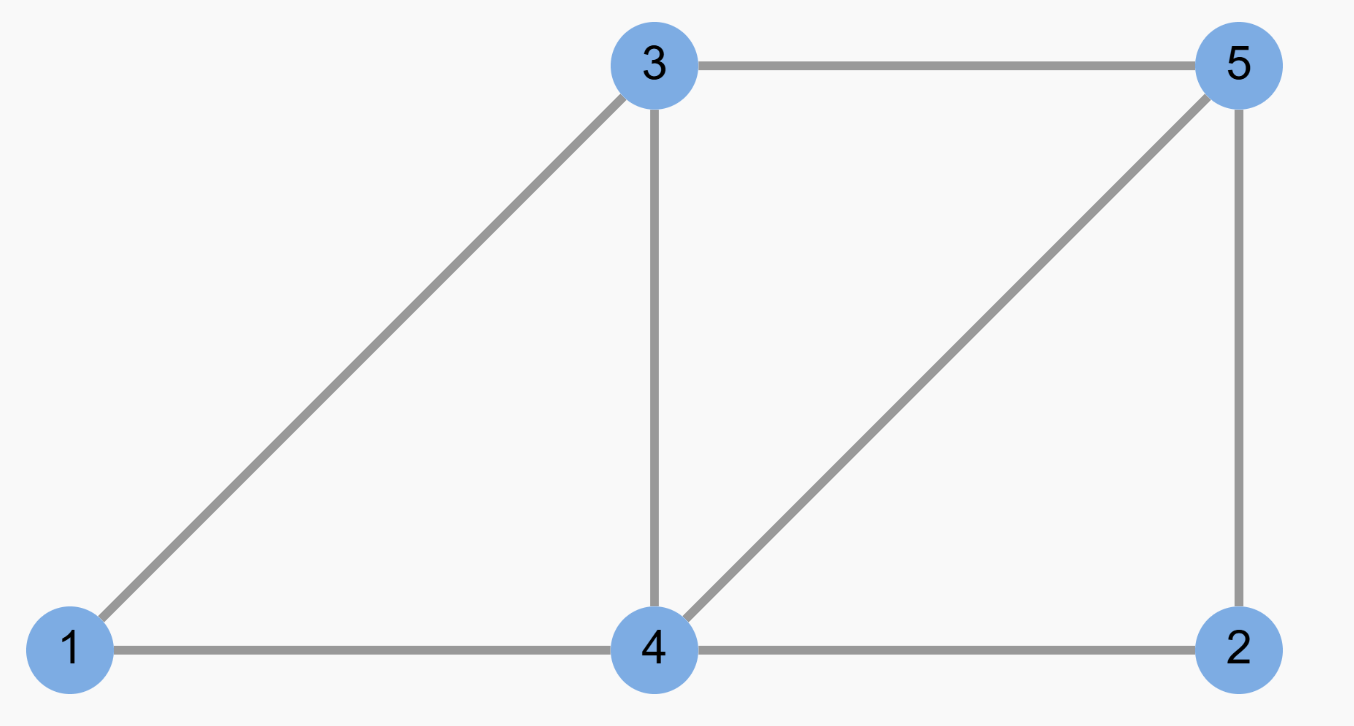
图中节点 1 和节点 3 之间有一条无向边,这说明可以从节点 1 到达节点 3,也可以从节点 3 到达节点 1。
你可以把无向图理解成「双向图」,实际上我们在用代码实现图结构的时候就是这么做的。
下图是一个有向加权图:

下图是一个无向加权图:
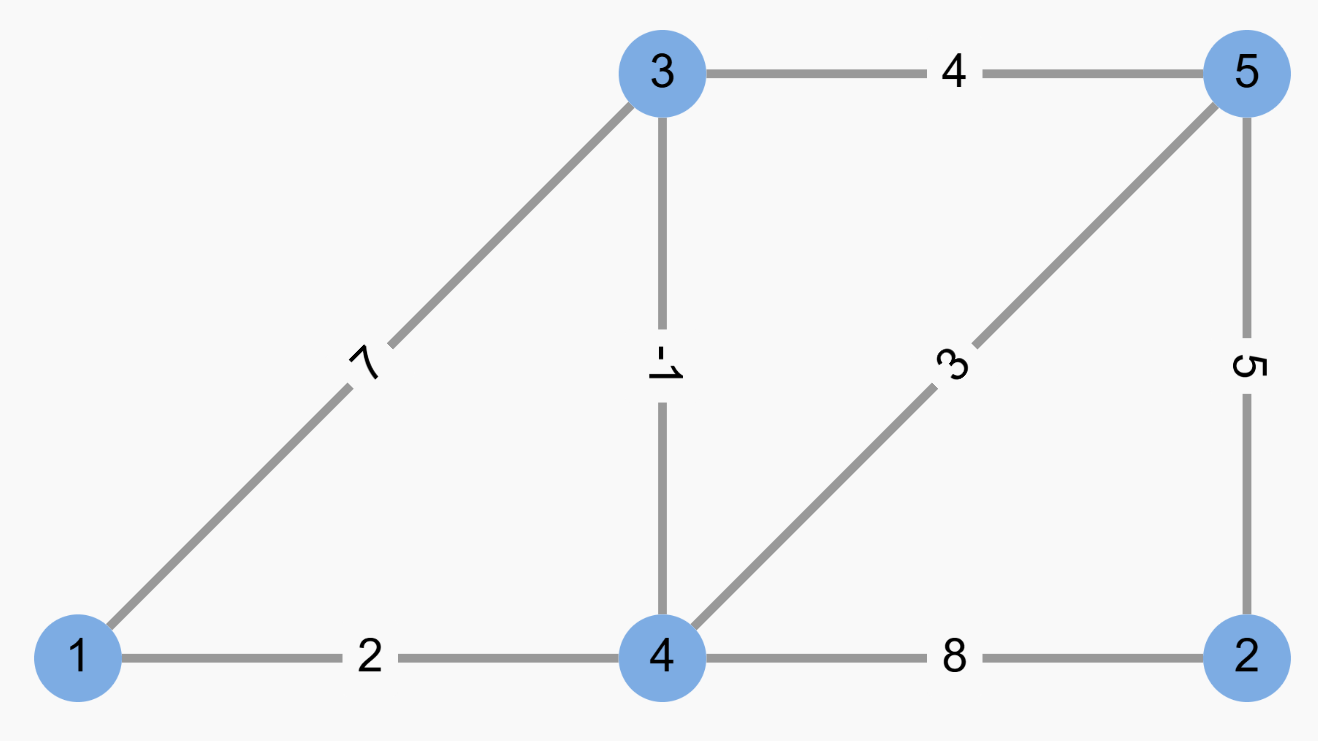
加权图在实际场景中非常常见,比如在地图 App 中,边的权重可以是两个地点之间的距离;在物流网络中,边的权重可以是两个地点之间的运输成本等等。
围绕着加权图,又会有很多经典的图论算法,比如计算最短路径,最小生成树等等,这些都会在后面的章节逐步讲解。
度
对于图中的每个节点,有一个度 (degree) 的概念。
在无向图中,度就是每个节点相连的边的条数。
比方下面这幅无向图中,节点 1 的度为 2,节点 4 的度为 4。

由于有向图的边有方向,所以有向图中每个节点的度被细分为入度 (indegree)和出度(outdegree)。
比如下图中节点 3 的入度为 2(有两条边指向它),出度为 1(它有 1 条边指向别的节点):

边和节点的数量关系
我们一般讨论的图结构都是简单图(Simple Graph),即没有自环边(Self loop)和多重边(Multiple edges)的图。
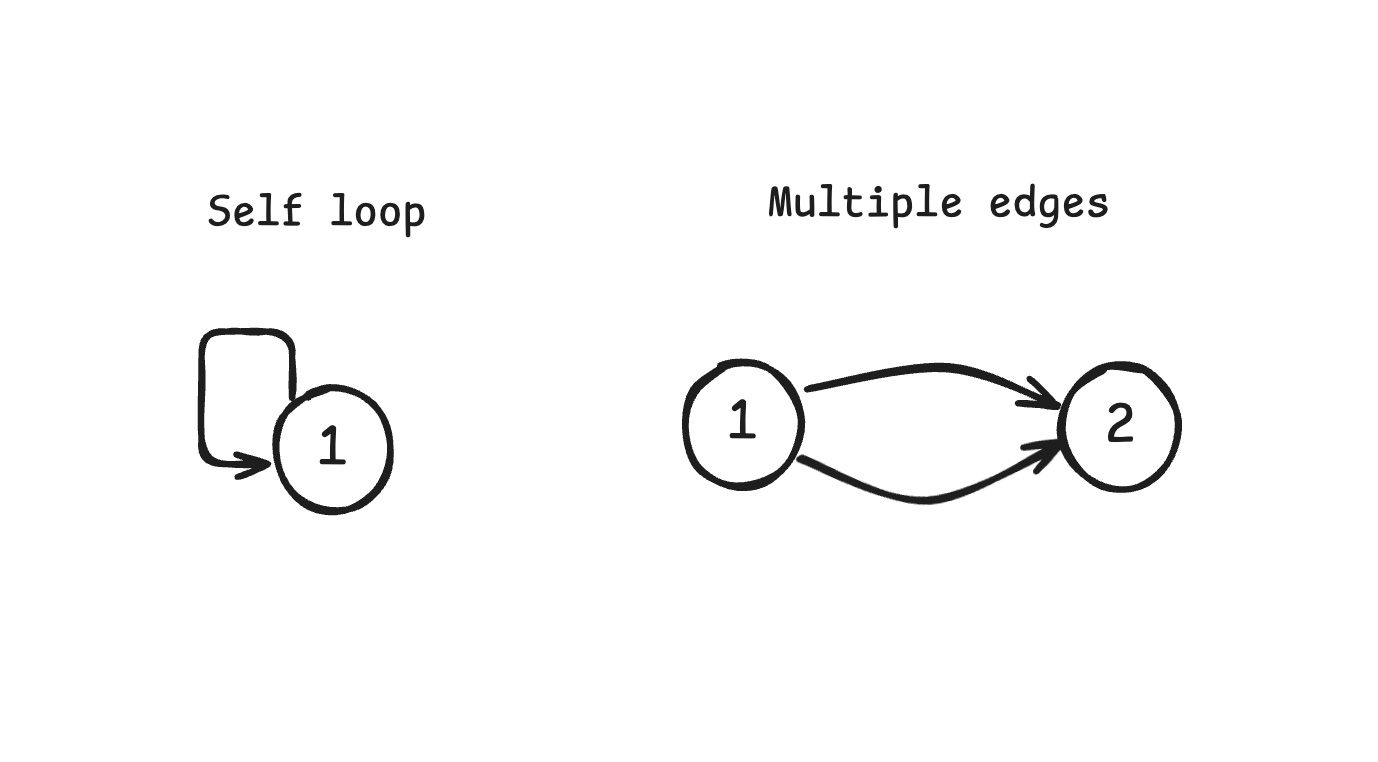
在简单图中,假设包含 E 条边,V 个节点,我们想一下边的条数 E 的取值范围是多少? E 的最小值可以是 0,相当于图结构中只有若干互不相连的节点,这是可以的。
考虑 E 的最大值,图中的每个节点最多可以有 V−1 条边与其他 V−1 个节点相连,所以最多能有的边数为 E=V(V−1)/2≈V² 。
如果 E 接近 V²,我们说这幅图是 稠密图(Dense Graph);如果 E 远小于 V²,我们说这幅图是 稀疏图(Sparse Graph)。
子图
在图论中,子图是一个重要的基本概念。
子图 (Subgraph):如果图 G′的所有节点和边都包含在图 G 中,则称 G′是 G 的一个子图。简单来说,子图是从原图中删除一些节点和边后得到的图。
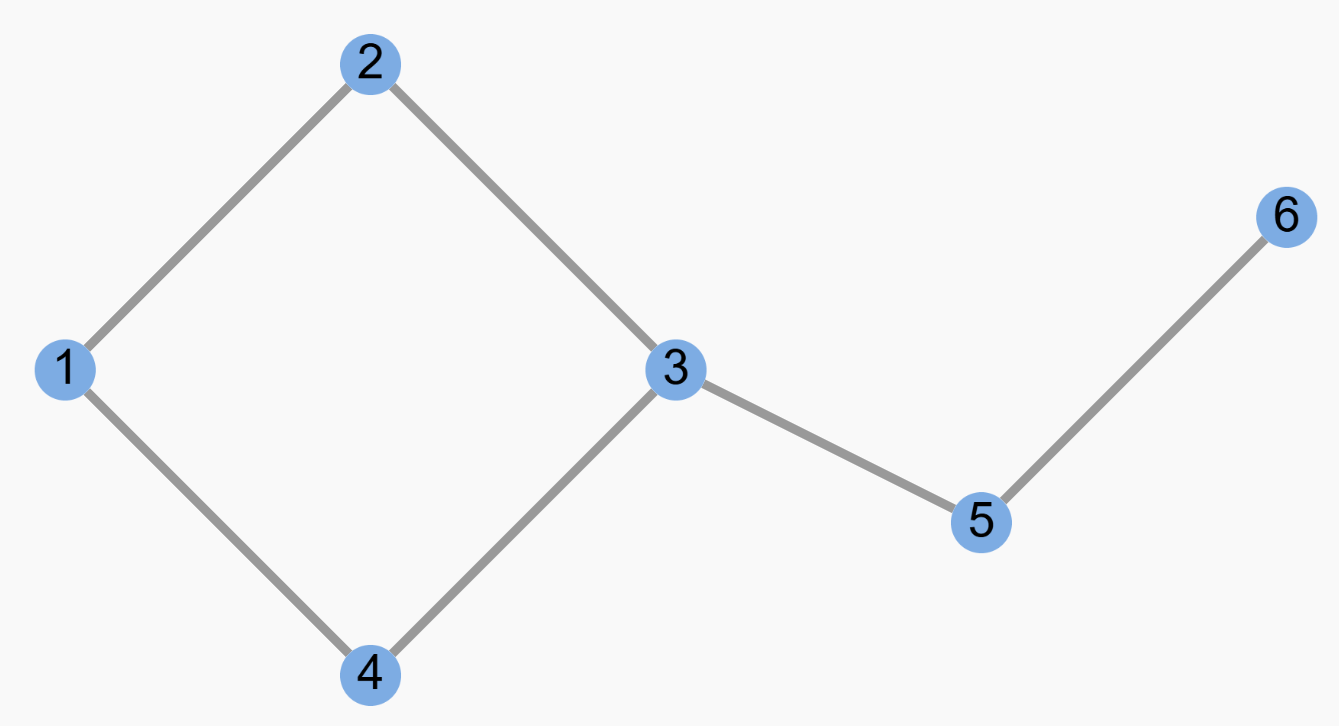
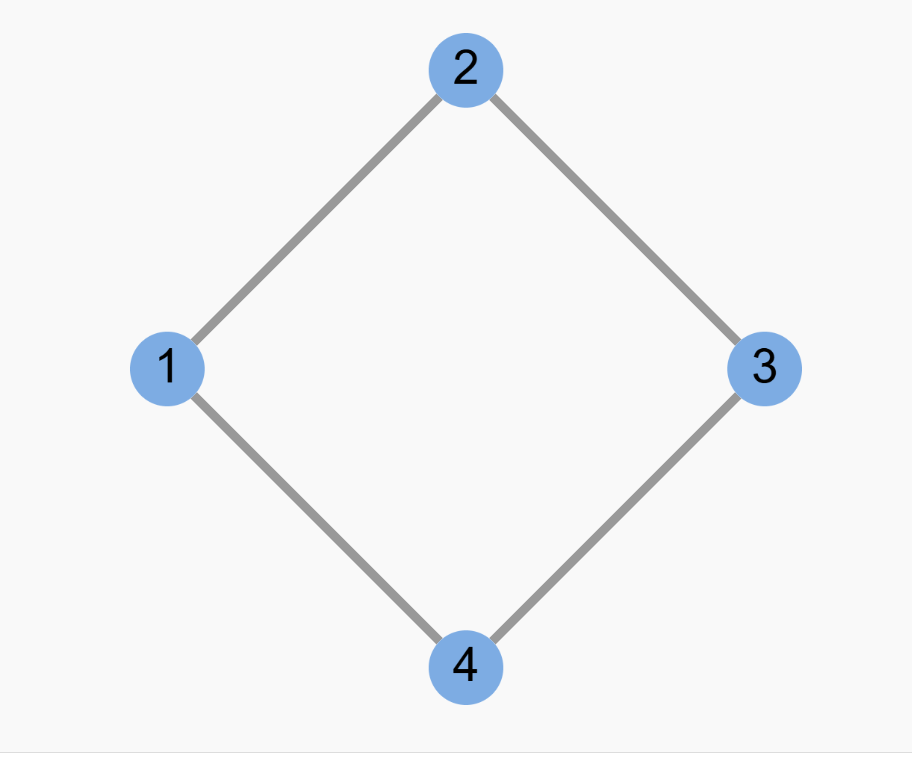
假设上面这幅图为 G,我们举例说明子图的概念。子图有两种特殊类型:
生成子图 (Spanning Subgraph):包含原图中所有节点,但只包含部分边的子图。
下图是图 G 的一个生成子图,它包含了所有节点,但移除了节点 3 和节点 4 之间的边。
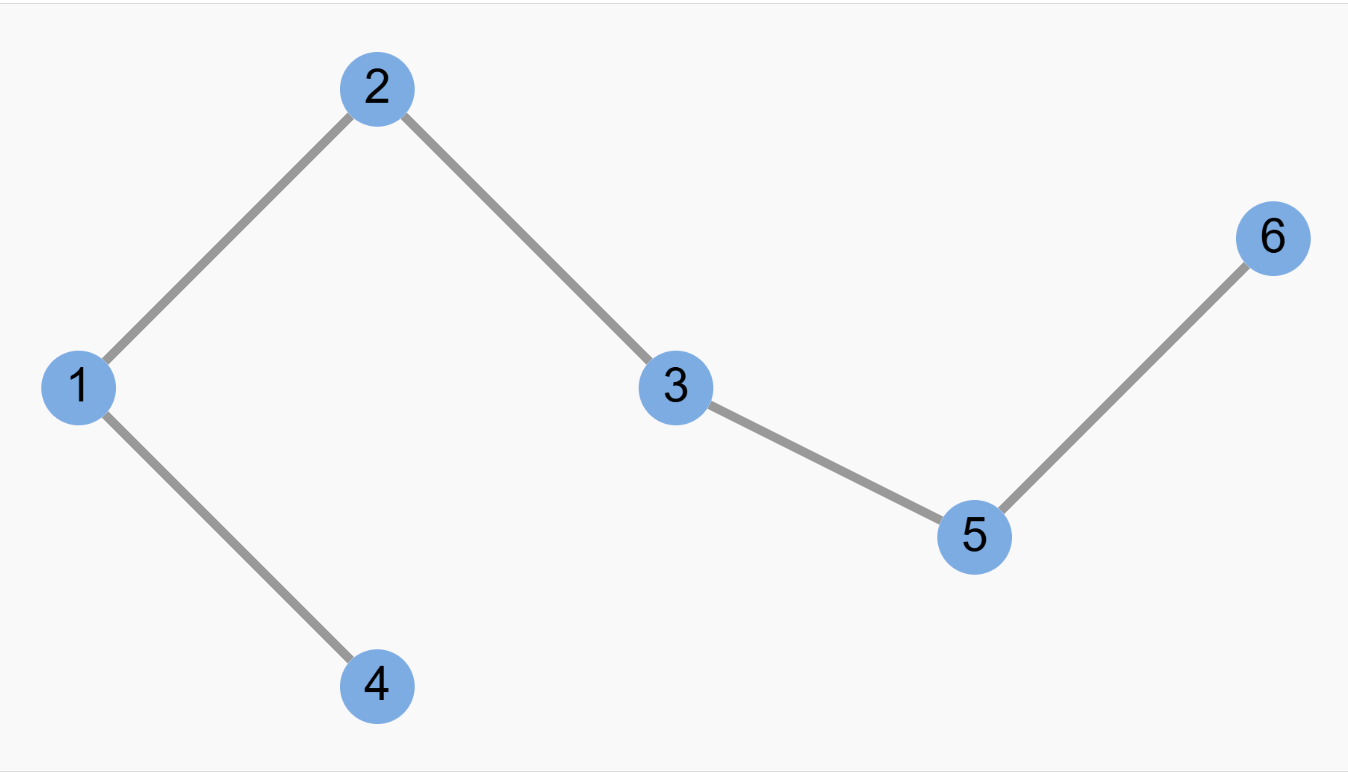
导出子图 (Induced Subgraph):选择原图的一部分节点,以及这些节点之间在原图中的所有边所构成的子图。
下图是图 G 的一个导出子图,它包含节点 1,2,3,4 及它们之间在原图中的所有边。
子图的概念在很多图算法中都有应用,比如在寻找最小生成树时,我们实际上是在寻找一个包含所有节点的带权重最小的生成子图。
连通性
在图论中,连通性是一个非常重要的概念,它描述了图中节点之间是否存在路径。
无向图的连通性
连通图 (Connected Graph): 如果无向图中任意两个节点之间都存在一条路径,我们称这个图是连通的。

上图是一个连通图,从任意一个节点出发,都能到达其他所有节点。
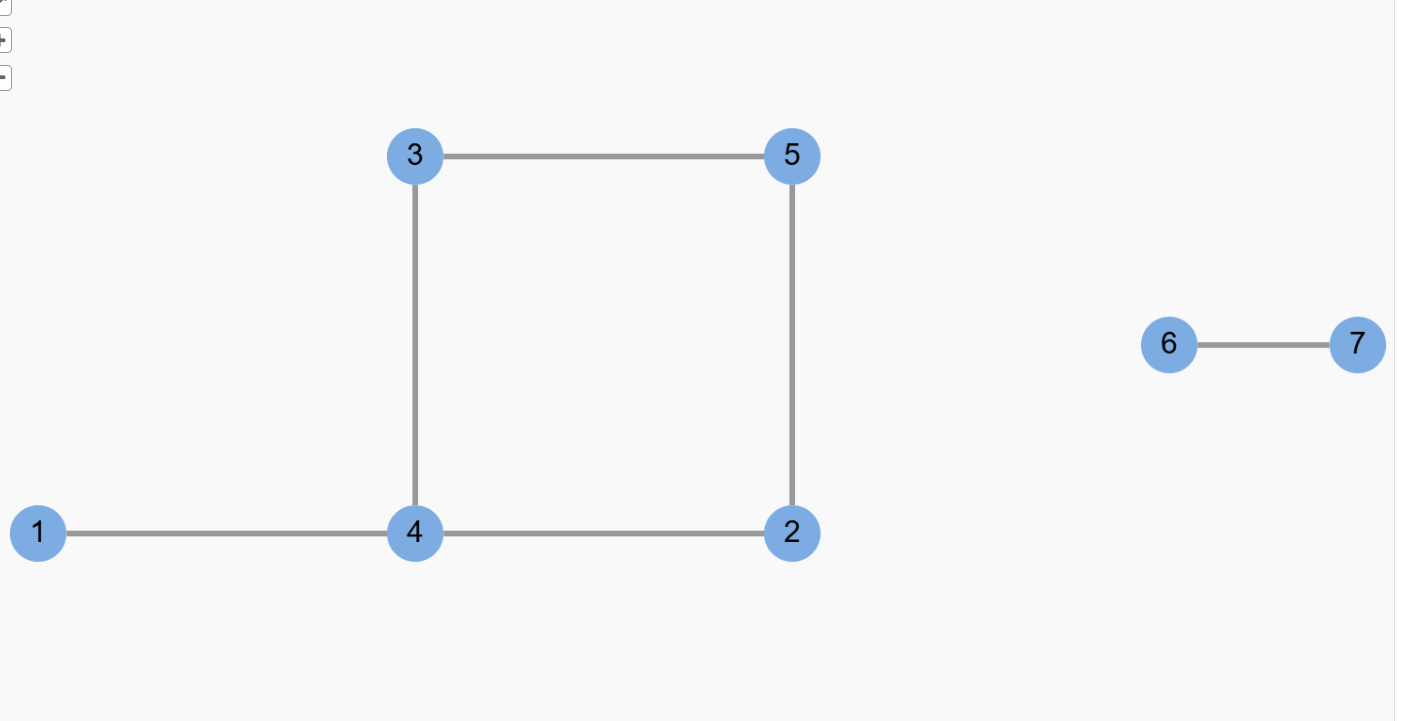
连通分量 (Connected Component):对于非连通的无向图,其中的多个连通子图被称为连通分量,一个图可以有多个连通分量。
比如下面这幅图有两个连通分量:节点 1~5 形成一个连通分量,节点 6,7 形成另一个连通分量。
有向图的连通性
有向图的连通性概念稍微复杂一些,因为考虑到边的方向,所以有向图的连通性分为强连通和弱连通。
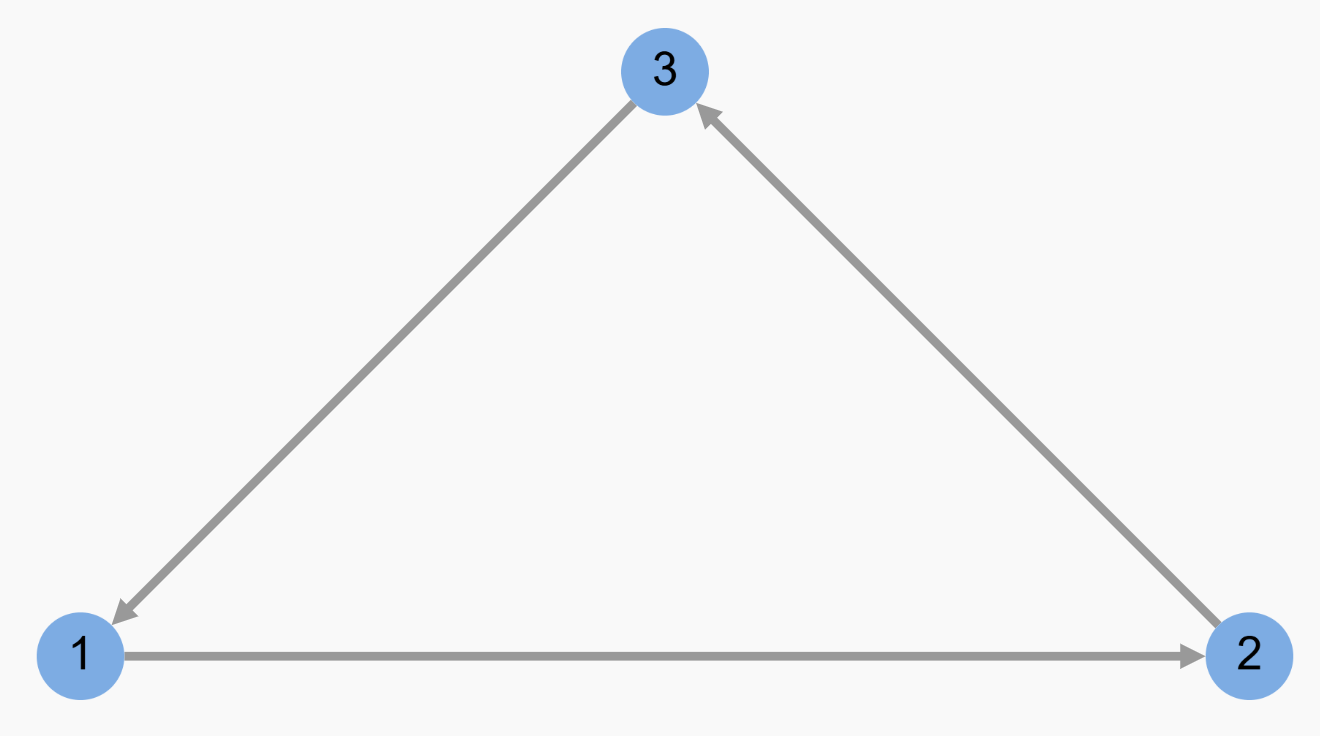
强连通图 (Strongly Connected Graph):如果有向图中任意两个节点之间都存在一条有向路径,我们称这个图是强连通的。
比如下面这幅图是一个强连通图,从任意节点出发都能到达其他所有节点。
弱连通图 (Weakly Connected Graph):如果将有向图中的所有有向边都变成无向边后,该图变成连通的,那么原来的有向图就是弱连通的。
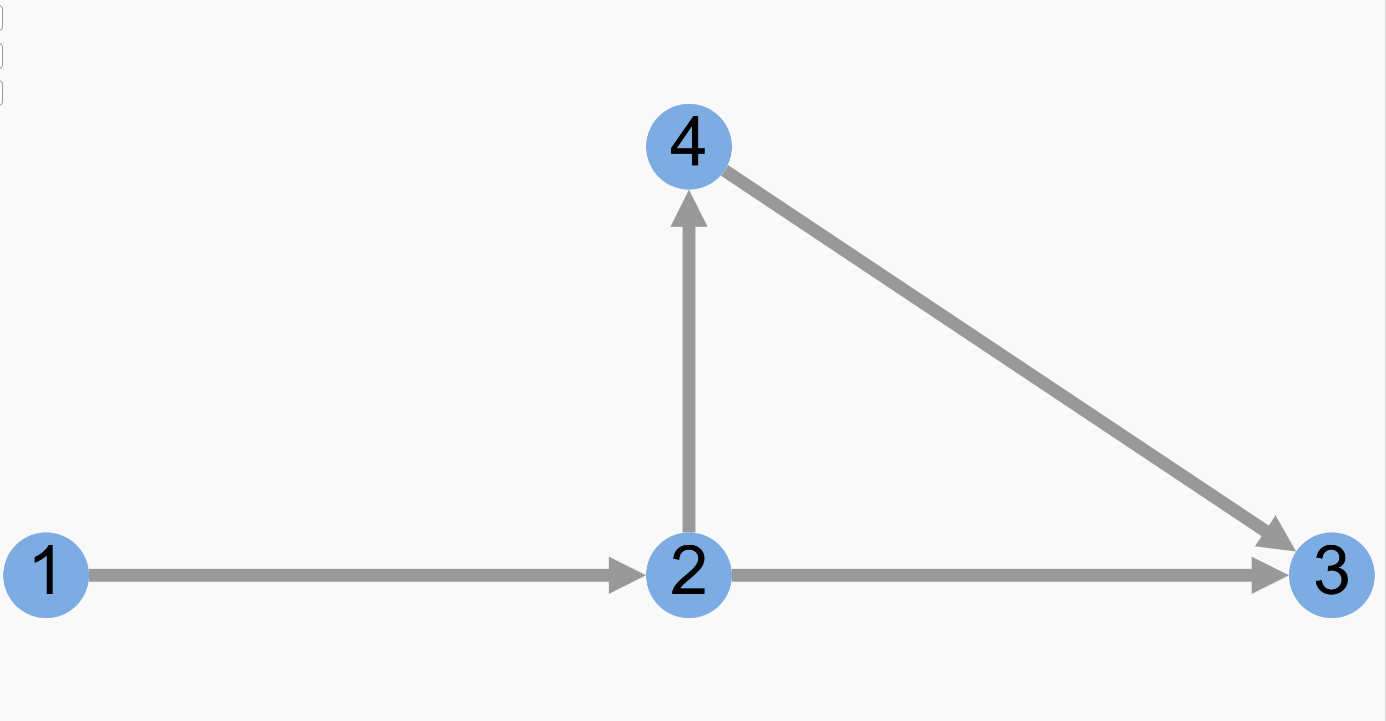
比如下面这幅图不是强连通的(无法从节点 4 到达节点 1),但它是弱连通的,因为忽略边的方向后,所有节点之间都是连通的。
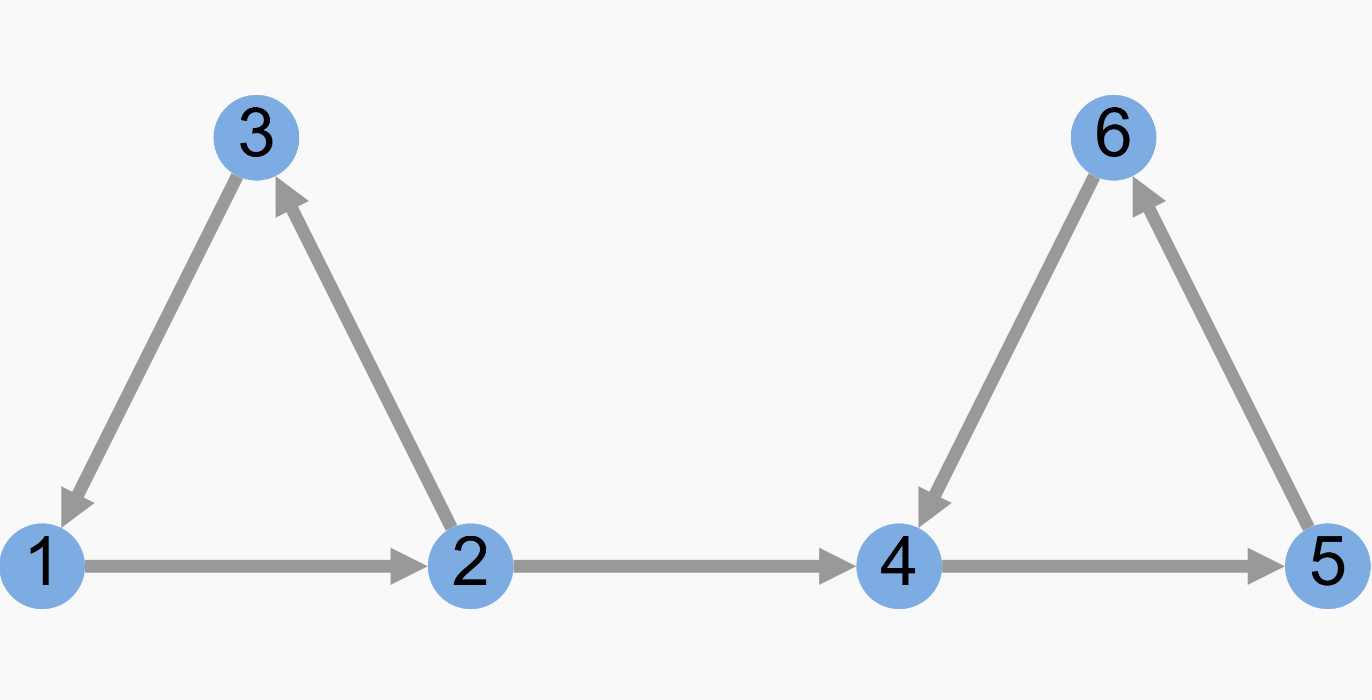
强连通分量 (Strongly Connected Component, SCC):有向图中的若干个最大的强连通子图称为强连通分量。
比如下面这幅图有两个强连通分量:节点 1~3 形成一个强连通分量,节点 4~6 形成另一个强连通分量。
弱连通分量 (Weakly Connected Component, WCC):将有向图的所有有向边变为无向边后,形成的连通分量称为原有向图的弱连通分量。
图论中还有很多其他的复杂术语,不过对于数据结构和算法的学习,理解上面这些名词就绰绰够用了。后面我们讲到具体的图论算法时,会结合实际场景运用这些概念。