数据压缩和霍夫曼树

本文会介绍霍夫曼编码的原理，并对比几种常见的数据压缩思路。

具体的代码实现会放到数据结构设计章节中，带你基于霍夫曼编码实现一个压缩程序。

浅谈数据压缩

我们可以把数据压缩算法分为两大类，分别是 无损压缩 和 有损压缩。

无损压缩 是指压缩后的数据可以完全还原，不会丢失任何信息。

比如我们把若干文件打包成一个 zip 压缩包，这个 zip 所需的磁盘空间会更小，且解压后可以完全还原原始文件，这就叫无损压缩。

有损压缩 是指压缩后的数据会丢失一些信息，但是压缩率更高（即压缩后的数据占用空间更小）。

比如我们经常会有图片压缩的需求，有些图像处理工具能够在不明显影响图片质量的前提下，显著降低图片的磁盘占用空间，这就是有损压缩。

那么我们来思考几个问题。

1、有损压缩是怎么做到在丢失信息的前提下，依然保证图片质量的呢？

2、有损压缩会丢失一些信息，换取空间的减少，这个可以理解。但无损压缩是怎么做到不丢失任何信息的前提下，压缩数据的呢？

首先，有损压缩肯定是会降低图片质量的，只不过这个降低的程度在我们的可接受范围内。

还是以图片压缩为例，人眼对「亮度」比较敏感，对「色度」不敏感。那么我们就可以用低精度的数据类型来表示「色度」，这样即便丢失了一些「色度」的信息，也几乎看不出区别。

但无损压缩不能这么搞，因为它要保证压缩后的数据可以再完全还原，所以无损压缩的本质就是编码和解码。

举个简单的例子，hahahahahahaha 这个字符串，我可以编码为 ha*7，解码时只需要把 ha 重复 7 次，就可以还原出原始字符串。

无损压缩的效果取决于压缩算法是否能够充分挖掘出原始数据中的冗余信息。

越是通用的压缩算法，能够挖掘出的冗余信息就越少，压缩率就越低；越是专用的压缩算法，能够挖掘出的冗余信息就越多，压缩率就越高。

比方说音频文件包含声波信息，专业的音频压缩算法能够找到声波信息中的冗余进行压缩，效果就好；而通用的 zip 压缩算法将音频文件也视为普通的字节流，无法挖掘声波信息的冗余，压缩效果自然就差。

所以没有全能的压缩算法，只能在通用性、压缩率和性能之间进行权衡。

本文讲解的霍夫曼编码，就是一种通用无损压缩算法，将原始数据输入霍夫曼算法，会得到压缩后的数据和一个码表，解码时需要根据码表还原出原始数据。

定长编码 vs 变长编码

既然说到了编码和解码，就不得不聊一聊定长编码（fixed-length encoding）和变长编码（variable-length encoding）。

ASCII 编码是一种定长编码，它将每个字符编码为 8 位二进制数，即一个字节。

UTF-8 编码是一种变长编码，它将每个字符编码为 1 到 4 个字节。

定长编码最大的优势是可以「随机访问」，因为每个字符的编码长度都是固定的，所以可以很容易地根据索引计算出字符的位置。

变长编码的优势是存储效率高，比如 UTF-8 编码就是一种变长编码，存储英文字符时占用一个字节，存储中文时占用三个字节，通用性和存储效率都比 ASCII 编码强。但由于每个字符的编码长度不固定，无法通过索引进行「随机访问」。

到这里不妨思考一下，现代编辑器基本都是用 UTF-8 编码了，而对字符串进行随机访问又是编辑器的基本功能，如果每次访问都要线性扫描，显然效率很差，那么编辑器是怎么解决这个问题的呢？

回到数据压缩的场景，比方说 aaabacc 这个字符串有 7 个小写字母，用 ASCII 编码需要 7x8=56 bit，我现在想对它进一步压缩，应该怎么做？

因为现在只有 a,b,c 三种字符，所以其实不需要用 8 比特来表示每个字符，用 2 比特就够了。

比方说这样编码：

a 编码为 00
b 编码为 01
c 编码为 10 那么 aaabacc 就可以编码为二进制的 00000001001010，长度为 14 比特。

这种编码方式就叫 定长编码，因为每个字符的编码长度都固定为 2 比特。

定长编码的好处是简单，只需要知道所有可能的字符种类，就可以确定编码了。不过定长编码的压缩效果并不是很好，因为没有充分利用字符出现的频率信息。

比方说还以 aaabacc 为例，既然字符 a 出现的频率较高，b,c 出现的频率低，那么能否使用更短的编码来表示 a，让 b,c 使用更长的编码呢？

其实是可以的，这就叫变长编码。比如这样编码：

a 编码为 0
b 编码为 10
c 编码为 11 那么 aaabacc 就可以编码为二进制的 0001001111，长度为 11 比特，比定长编码的压缩效果更好。

变长编码的难点

```md` 两个难点

1、如何设计编码才能保证解码的唯一性？

2、如何保证压缩率（编码数据尽可能短）？

3、如何保证解码的效率？ ``

我们仔细分析一下上面 aaabacc 的例子。

这种编码方案是没有歧义的：

a 编码为 0
b 编码为 10
c 编码为 11 如果把 a 编码为 1，那么编码方案中 a 和 c 的编码存在歧义：
a 编码为 1
b 编码为 10
c 编码为 11 aaabacc 会被编码为二进制的 11111011111，但是 a 和 c 的编码存在歧义，11 既可以解码为 c，也可以解码为 aa，所以无法解码出原始数据。

对比上面两个例子可以发现一些规律：任意一个编码，都不能是另一个编码的前缀。

比如第二个例子中， a 编码为 1，而 b, c 编码的前缀都是1，所以编码方案有歧义。

那么可能有读者会反驳，比如下面这个编码方案：

a 编码为 1
b 编码为 10
c 编码为 100 虽然出现了相同的前缀，但是我们可以在解码时添加额外的比较逻辑：

读取到 1 时，继续向后探测两位，看看是否可能凑出 10 或 100，进而决定如何解码。

这样确实可以保证解码唯一性，但是压缩率低，且解码效率差。向后匹配的逻辑相当于嵌套 for 循环：

for (int i = 0; i < N; i++) {
    for (int j = 1; j <= K; j++) {
        ...
    }
}

假设最长的编码长度为 K，编码后的数据长度为 N，那么解码的时间复杂度 O(NK)。

如果你能保证任意一个编码都不是另一个编码的前缀，那么就不需要尝试向后匹配了。这样一来，解码的复杂度就降到了 O(N)。

在实际的编解码场景中 N 往往很大，即便 K 较小，解码速度慢几倍也是非常糟糕的，所以我们需要保证编解码算法的时间复杂度为 O(N)，且压缩率尽可能高。

霍夫曼编码原理

霍夫曼编码就是一种变长编码方案，它借助二叉树结构构造变长编码，能够确保解码的唯一性，同时兼顾压缩效果和性能。

首先让我们来研究这样一棵二叉树：

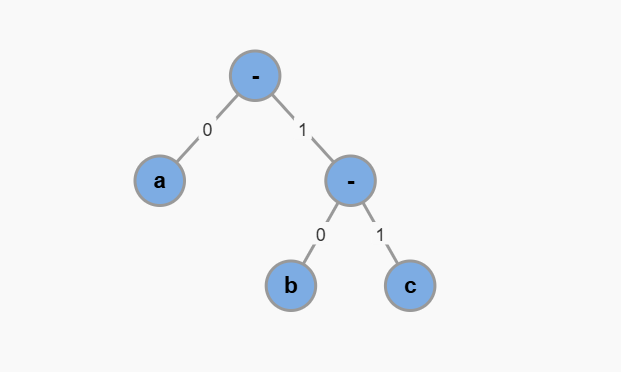
hufuman1

在上面这棵二叉树中，每个二叉树节点的左侧树枝代表 0，右侧树枝代表 1，叶子节点就是每个待编码的字符，从根节点到叶子节点经过的 0,1 序列就是该字符的编码：

a -> 0
b -> 10
c -> 11

由于每个字符都处于叶子节点，所以任意一个编码都不可能是另一个编码的前缀，必然不存在解码歧义，且解码时也不需要多余的探测逻辑，时间复杂度为 O(N)。

唯一剩下的问题就是，如何才能保证压缩率尽可能高？

来看一个稍微复杂的场景，假设一个字符串包含 a, b, c, d, e五种字符，它们可以构造出下面这棵二叉树：

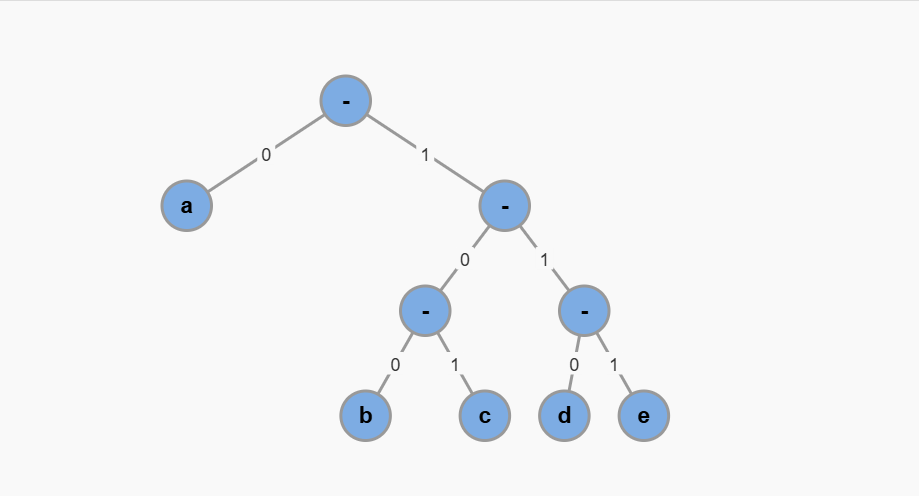
huofuman2

每个字符的编码如下：

a -> 0
b -> 100
c -> 101
d -> 110
e -> 111

但我们也可以修改一下这棵二叉树的形态，变成这样：

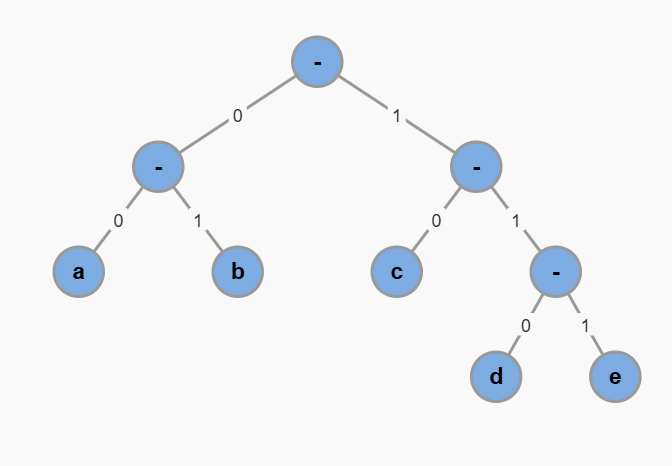
huofuman3

对应的编码方案是：

a -> 00
b -> 01
c -> 10
d -> 110
e -> 111

显然，到底哪种编码方案的压缩率最好，取决于每个字符出现的频率。

我们可以把每个字符出现的频率也存储到二叉树的叶子节点，假设是这样：

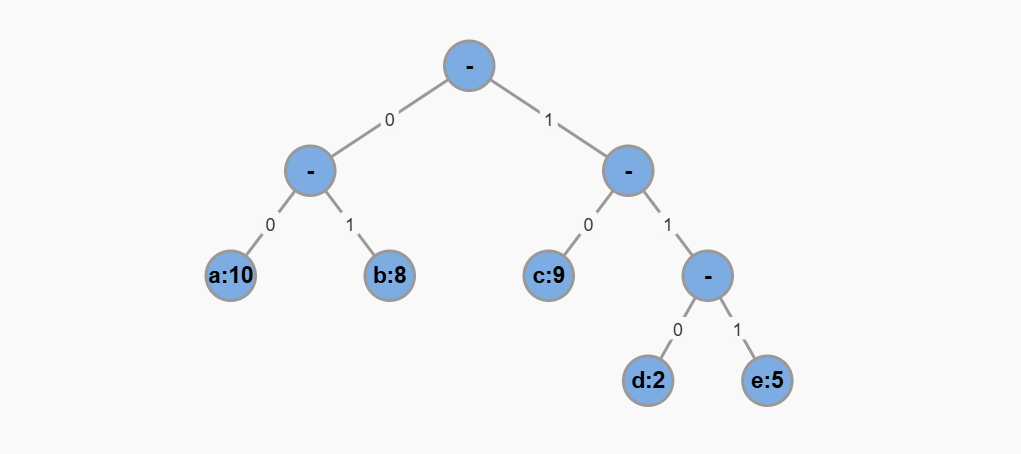
huofuman4

那么编码后的数据长度应该就是：叶子节点的值乘以从根节点到该叶子节点的路径长度，最后对所有叶子节点求和。这就是 树的带权路径长度（Weighted Path Length），简称 WPL。

上面的示例中，树的带权路径长度为：

10 * 2 + 8 * 2 + 9 * 2 + 2 * 3 + 5 * 3 = 75

我们想让编码后的数据长度尽可能短，其实就是寻找一棵 WPL 最小的二叉树，这棵树就叫做最优前缀编码树或霍夫曼树（Huffman Tree）。基于这棵树计算出的编码方案，就是霍夫曼编码（Huffman Coding）。

构造霍夫曼树的思路也不难想到，关键就是要把出现频率高的字符放在离根节点较近的地方，把出现频率低的字符放在离根节点较远的地方。

具体的代码实现会更新到数据结构设计章节具体介绍，这里暂不展开。