二叉堆/优先级队列代码实现

前文二叉堆的原理介绍了二叉堆的基本性质、API 和常见应用。

我们先实现一个简化版的优先级队列，用来帮你理解二叉堆的核心操作 sink 和 swim。最后我再用给出一个比较完整的代码实现。

简化版优先级队列

我们实现的这个简化版优先级队列有如下限制：

1、不支持泛型，仅支持存储整数类型的元素。

2、不考虑扩容的问题，队列的容量在创建时固定，假设插入的元素数量不会超过这个容量。

3、底层仅实现一个小顶堆（即根节点是整个堆中的最小值），不支持自定义比较器。

基于上面这些限制，这个简化版优先级队列的 API 如下：

java:

class SimpleMinPQ {
    // 创建一个容量为 capacity 的优先级队列
    public SimpleMinPQ(int capacity);

    // 返回队列中的元素个数
    public int size();

    // 向队列中插入一个元素
    public void push(int x);

    // 返回队列中的最小元素（堆顶元素）
    public int peek();

    // 删除并返回队列中的最小元素（堆顶元素）
    public int pop();
}

// 使用方法
SimpleMinPQ pq = new SimpleMinPQ(10);
pq.push(3);
pq.push(4);
pq.push(1);
pq.push(2);
System.out.println(pq.pop()); // 1
System.out.println(pq.pop()); // 2
System.out.println(pq.pop()); // 3
System.out.println(pq.pop()); // 4

go:

type SimpleMinPQ struct {
    // 创建一个容量为 capacity 的优先级队列
    SimpleMinPQ(capacity int)

    // 返回队列中的元素个数
    Size() int

    // 向队列中插入一个元素
    Push(x int)

    // 返回队列中的最小元素（堆顶元素）
    Peek() int

    // 删除并返回队列中的最小元素（堆顶元素）
    Pop() int
}

// 使用方法
pq := SimpleMinPQ(10)
pq.Push(3)
pq.Push(4)
pq.Push(1)
pq.Push(2)
fmt.Println(pq.Pop()) // 1
fmt.Println(pq.Pop()) // 2
fmt.Println(pq.Pop()) // 3
fmt.Println(pq.Pop()) // 4

难点分析 在前文二叉堆的原理中你应该也感觉到了，二叉堆的难点在于你在插入或删除元素时，还要保持堆的性质。

具体来说，看下面这个可视化面板，我在这个小顶堆中调用 push 方法插入元素 4，然后再调用 pop 方法删除堆顶元素 0。

请你先点击 let minHeap 这部分代码，让最小堆以及初始元素构造出来。注意看每个二叉树节点的值都比它的两个子树上的节点的值小，满足小顶堆的性质。

然后点击 push(4) 那行代码，可以看到这个新元素 4 被插入到了原先 6 的位置，而 6 被下沉为 4 的子节点，这样依然保持了小顶堆的性质。如果你直接把 4 放到树的最下层的话，比如作为 6 的子节点，就不满足小顶堆的性质了。

最后点击 pop() 那行代码，可以看到堆顶元素 0 被删除，元素 1 取代了 0 的位置作为新的堆顶元素，而 6 被从最左侧移动元素 1 原先的位置。这样依然保持了小顶堆的性质。

增：push/swim 方法插入元素

核心步骤

以小顶堆为例，向小顶堆中插入新元素遵循两个步骤：

1、先把新元素追加到二叉树底层的最右侧，保持完全二叉树的结构。此时该元素的父节点可能比它大，不满足小顶堆的性质。

2、为了恢复小顶堆的性质，需要将这个新元素不断上浮（`swim`），直到它的父节点比它小为止，或者到达根节点。此时整个二叉树就满足小顶堆的性质了。

删：pop/sink 方法删除元素

核心步骤

以小顶堆为例，删除小顶堆的堆顶元素遵循两个步骤：

1、先把堆顶元素删除，把二叉树底层的最右侧元素摘除并移动到堆顶，保持完全二叉树的结构。此时堆顶元素可能比它的子节点大，不满足小顶堆的性质。

2、为了恢复小顶堆的性质，需要将这个新的堆顶元素不断下沉（sink），直到它比它的子节点小为止，或者到达叶子节点。此时整个二叉树就满足小顶堆的性质了。

查：peek 方法查看堆顶元素

在数组上模拟二叉树 在之前的所有内容中，我都把二叉堆作为一种二叉树来讲解，而且可视化面板中也是通过操作 HeapNode 节点的方式来展示的。但实际上，我们在代码实现的时候，不会用类似 HeapNode 的节点类来实现，而是用数组来模拟二叉树结构。

用数组模拟二叉树的原因

第一个原因是前面介绍
数组 和
链表 时说到的，链表节点需要一个额外的指针存储相邻节点的地址，所以相对数组，链表的内存消耗会大一些。我们这里的 HeapNode 类也是链式存储的例子，和链表节点类似，需要额外的指针存储父节点和子节点的地址。

第二个原因，也是最主要的原因，是时间复杂度的问题。仔细想一下前面我给你展示的 push 和 pop 方法的操作过程，它们的第一步是什么？是不是要找到二叉树最底层的最右侧元素？

因为上面举的场景是我们自己构造的，可以直接用操作 left, right 指针的方式把目标节点拿到。但你想想，正常情况下你如何拿到二叉树的底层最右侧节点？你需要层序遍历或递归遍历二叉树，时间复杂度是 O(N)，进而导致 push 和 pop 方法的时间复杂度退化到 O(N)，这显然是不可接受的。

如果用数组来模拟二叉树，就可以完美解决这个问题，在 O(1) 时间内找到二叉树的底层最右侧节点。

完全二叉树是关键

想要用数组模拟二叉树，前提是这个二叉树必须是完全二叉树。

我在二叉树基础中介绍过完全二叉树，就是除了最后一层，其他层的节点都是满的，最后一层的节点都靠左排列。

由于完全二叉树上的元素都是紧凑排列的，我们可以用数组来存储。

直接在数组的末尾追加元素，就相当于在完全二叉树的最后一层从左到右依次填充元素；数组中最后一个元素，就是完全二叉树的底层最右侧的元素，完美契合我们实现二叉堆的场景。

看这幅图就明白了：

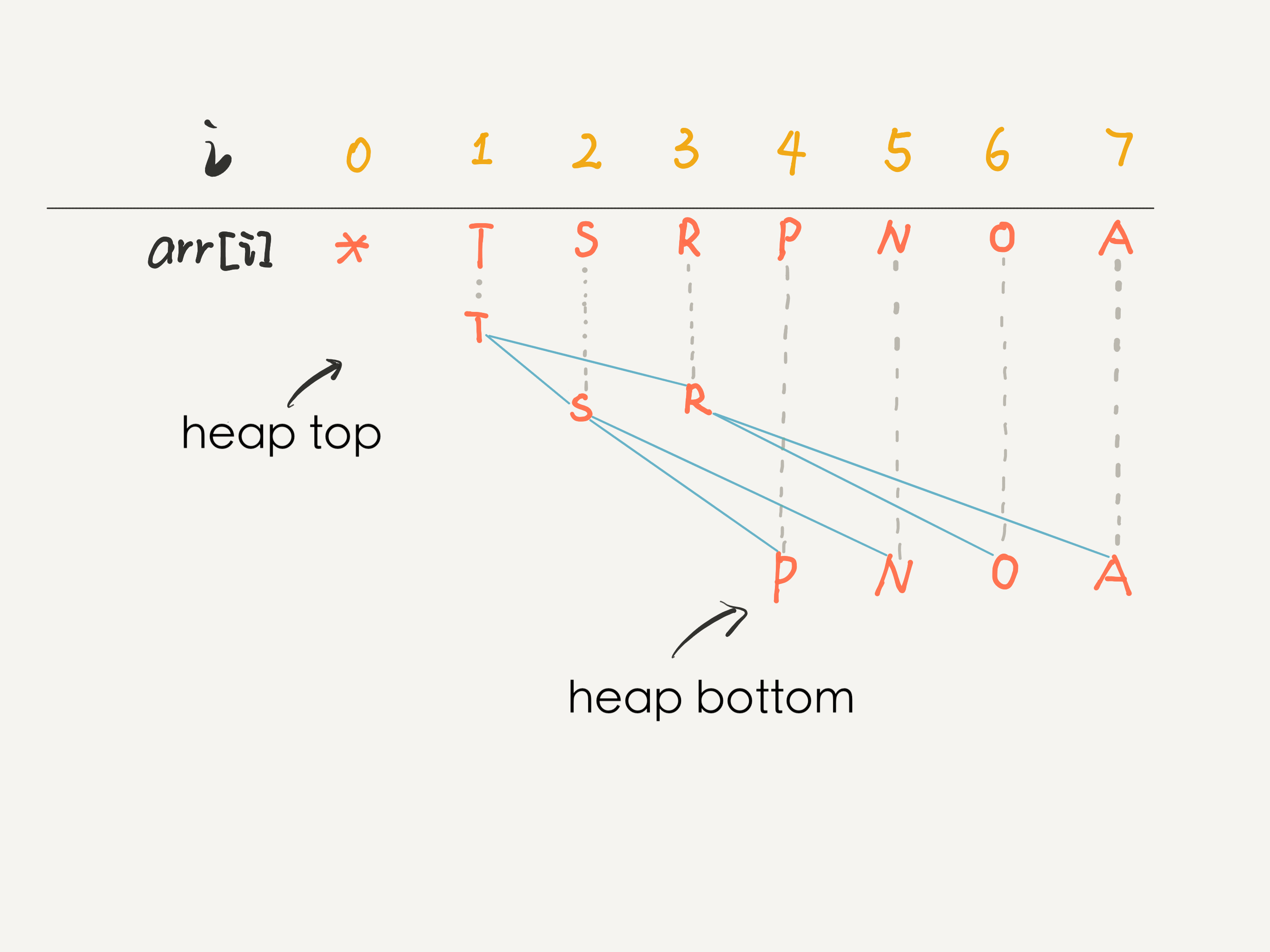
erchashuyouxianji

在这个数组中，索引 0 空着不用，就可以根据任意节点的索引计算出父节点或左右子节点的索引： java:

// 父节点的索引
int parent(int node) {
    return node / 2;
}
// 左子节点的索引
int left(int node) {
    return node * 2;
}
// 右子节点的索引
int right(int node) {
    return node * 2 + 1;
}

go:

// 父节点的索引
func parent(node int) int {
    return node / 2
}

// 左子节点的索引
func left(node int) int {
    return node * 2
}

// 右子节点的索引
func right(node int) int {
    return node * 2 + 1
}

有读者会问，为啥数组中索引 0 要空着不用，从 1 开始存储元素呢？

其实从 0 开始也是可以的，稍微改一改计算公式就行了：

erchashuyouxianji2 java:

// 父节点的索引
int parent(int node) {
    return (node - 1) / 2;
}

// 左子节点的索引
int left(int node) {
    return node * 2 + 1;
}

// 右子节点的索引
int right(int node) {
    return node * 2 + 2;
}

go:

// 父节点的索引
func parent(node int) int {
    return (node - 1) / 2
}

// 左子节点的索引
func left(node int) int {
    return node * 2 + 1
}

// 右子节点的索引
func right(node int) int {
    return node * 2 + 2
}

代码实现

下面是一个简化版的小顶堆优先级队列核心逻辑的实现，没有特别处理边界情况，供你参考： java:

public class SimpleMinPQ {
    // 底层使用数组实现二叉堆
    private final int[] heap;

    // 堆中元素的数量
    private int size;

    public SimpleMinPQ(int capacity) {
        heap = new int[capacity];
        size = 0;
    }

    public int size() {
        return size;
    }

    // 父节点的索引
    private int parent(int node) {
        return (node - 1) / 2;
    }

    // 左子节点的索引
    private int left(int node) {
        return node * 2 + 1;
    }

    // 右子节点的索引
    private int right(int node) {
        return node * 2 + 2;
    }

    // 交换数组的两个元素
    private void swap(int i, int j) {
        int temp = heap[i];
        heap[i] = heap[j];
        heap[j] = temp;
    }

    // 查，返回堆顶元素，时间复杂度 O(1)
    public int peek() {
        return heap[0];
    }

    // 增，向堆中插入一个元素，时间复杂度 O(logN)
    public void push(int x) {
        // 把新元素追加到最后
        heap[size] = x;
        // 然后上浮到正确位置
        swim(size);
        size++;
    }

    // 删，删除堆顶元素，时间复杂度 O(logN)
    public int pop() {
        int res = heap[0];
        // 把堆底元素放到堆顶
        heap[0] = heap[size - 1];
        size--;
        // 然后下沉到正确位置
        sink(0);
        return res;
    }

    // 上浮操作，时间复杂度是树高 O(logN)
    private void swim(int node) {
        while (node > 0 && heap[parent(node)] > heap[node]) {
            swap(parent(node), node);
            node = parent(node);
        }
    }

    // 下沉操作，时间复杂度是树高 O(logN)
    private void sink(int node) {
        while (left(node) < size || right(node) < size) {
            // 比较自己和左右子节点，看看谁最小
            int min = node;
            if (left(node) < size && heap[left(node)] < heap[min]) {
                min = left(node);
            }
            if (right(node) < size && heap[right(node)] < heap[min]) {
                min = right(node);
            }
            if (min == node) {
                break;
            }
            // 如果左右子节点中有比自己小的，就交换
            swap(node, min);
            node = min;
        }
    }

    public static void main(String[] args) {
        SimpleMinPQ pq = new SimpleMinPQ(5);
        pq.push(3);
        pq.push(2);
        pq.push(1);
        pq.push(5);
        pq.push(4);

        System.out.println(pq.pop()); // 1
        System.out.println(pq.pop()); // 2
        System.out.println(pq.pop()); // 3
        System.out.println(pq.pop()); // 4
        System.out.println(pq.pop()); // 5
    }
}

go:

package main

import "fmt"

type SimpleMinPQ struct {
	// 底层使用数组实现二叉堆
	heap []int

	// 堆中元素的数量
	size int
}

// 父节点的索引
func (pq *SimpleMinPQ) parent(node int) int {
	return (node - 1) / 2
}

// 左子节点的索引
func (pq *SimpleMinPQ) left(node int) int {
	return node*2 + 1
}

// 右子节点的索引
func (pq *SimpleMinPQ) right(node int) int {
	return node*2 + 2
}

// 交换数组的两个元素
func (pq *SimpleMinPQ) swap(i, j int) {
	pq.heap[i], pq.heap[j] = pq.heap[j], pq.heap[i]
}

// 查，返回堆顶元素，时间复杂度 O(1)
func (pq *SimpleMinPQ) peek() int {
	return pq.heap[0]
}

// 增，向堆中插入一个元素，时间复杂度 O(logN)
func (pq *SimpleMinPQ) push(x int) {
	// 把新元素追加到最后
	pq.heap[pq.size] = x
	// 然后上浮到正确位置
	pq.swim(pq.size)
	pq.size++
}

// 删，删除堆顶元素，时间复杂度 O(logN)
func (pq *SimpleMinPQ) pop() int {
	res := pq.heap[0]
	// 把堆底元素放到堆顶
	pq.heap[0] = pq.heap[pq.size-1]
	pq.size--
	// 然后下沉到正确位置
	pq.sink(0)
	return res
}

// 上浮操作，时间复杂度是树高 O(logN)
func (pq *SimpleMinPQ) swim(node int) {
	for node > 0 && pq.heap[pq.parent(node)] > pq.heap[node] {
		pq.swap(pq.parent(node), node)
		node = pq.parent(node)
	}
}

// 下沉操作，时间复杂度是树高 O(logN)
func (pq *SimpleMinPQ) sink(node int) {
	for pq.left(node) < pq.size || pq.right(node) < pq.size {
		// 比较自己和左右子节点，看看谁最小
		min := node
		if pq.left(node) < pq.size && pq.heap[pq.left(node)] < pq.heap[min] {
			min = pq.left(node)
		}
		if pq.right(node) < pq.size && pq.heap[pq.right(node)] < pq.heap[min] {
			min = pq.right(node)
		}
		if min == node {
			break
		}
		// 如果左右子节点中有比自己小的，就交换
		pq.swap(node, min)
		node = min
	}
}

func main() {
	pq := SimpleMinPQ{
		heap: make([]int, 5),
		size: 0,
	}

	pq.push(3)
	pq.push(2)
	pq.push(1)
	pq.push(5)
	pq.push(4)

	fmt.Println(pq.pop()) // 1
	fmt.Println(pq.pop()) // 2
	fmt.Println(pq.pop()) // 3
	fmt.Println(pq.pop()) // 4
	fmt.Println(pq.pop()) // 5
}

明白了这个 SimpleMinPQ 类的实现，如果你想实现一个大顶堆 SimpleMaxPQ，只需要把 swim 和 sink 方法中元素大小比较的逻辑反过来即可，这里就不再赘述了。

完善版优先级队列

基于上面的简化版优先级队列，只要加上泛型、自定义比较器、扩容等功能，就可以实现一个比较完善的优先级队列了： java:

import java.util.Comparator;
import java.util.NoSuchElementException;

public class MyPriorityQueue<T> {
    private T[] heap;
    private int size;
    private final Comparator<? super T> comparator;

    @SuppressWarnings("unchecked")
    public MyPriorityQueue(int capacity, Comparator<? super T> comparator) {
        heap = (T[]) new Object[capacity];
        size = 0;
        this.comparator = comparator;
    }

    public int size() {
        return size;
    }

    public boolean isEmpty() {
        return size == 0;
    }

    // 父节点的索引
    private int parent(int node) {
        return (node - 1) / 2;
    }

    // 左子节点的索引
    private int left(int node) {
        return node * 2 + 1;
    }

    // 右子节点的索引
    private int right(int node) {
        return node * 2 + 2;
    }

    // 交换数组的两个元素
    private void swap(int i, int j) {
        T temp = heap[i];
        heap[i] = heap[j];
        heap[j] = temp;
    }

    // 查，返回堆顶元素，时间复杂度 O(1)
    public T peek() {
        if (isEmpty()) {
            throw new NoSuchElementException("Priority queue underflow");
        }
        return heap[0];
    }

    // 增，向堆中插入一个元素，时间复杂度 O(logN)
    public void push(T x) {
        // 扩容
        if (size == heap.length) {
            resize(2 * heap.length);
        }
        // 把新元素追加到最后
        heap[size] = x;
        // 然后上浮到正确位置
        swim(size);
        size++;
    }

    // 删，删除堆顶元素，时间复杂度 O(logN)
    public T pop() {
        if (isEmpty()) {
            throw new NoSuchElementException("Priority queue underflow");
        }
        T res = heap[0];
        // 把堆底元素放到堆顶
        swap(0, size - 1);
        // 避免对象游离
        heap[size - 1] = null;
        size--;
        // 然后下沉到正确位置
        sink(0);
        // 缩容
        if ((size > 0) && (size == heap.length / 4)) {
            resize(heap.length / 2);
        }
        return res;
    }

    // 上浮操作，时间复杂度是树高 O(logN)
    private void swim(int node) {
        while (node > 0 && comparator.compare(heap[parent(node)], heap[node]) > 0) {
            swap(parent(node), node);
            node = parent(node);
        }
    }

    // 下沉操作，时间复杂度是树高 O(logN)
    private void sink(int node) {
        while (left(node) < size || right(node) < size) {
            // 比较自己和左右子节点，看看谁最小
            int min = node;
            if (left(node) < size && comparator.compare(heap[left(node)], heap[min]) < 0) {
                min = left(node);
            }
            if (right(node) < size && comparator.compare(heap[right(node)], heap[min]) < 0) {
                min = right(node);
            }
            if (min == node) {
                break;
            }
            // 如果左右子节点中有比自己小的，就交换
            swap(node, min);
            node = min;
        }
    }

    // 调整堆的大小
    @SuppressWarnings("unchecked")
    private void resize(int capacity) {
        assert capacity > size;
        T[] temp = (T[]) new Object[capacity];
        for (int i = 0; i < size; i++) {
            temp[i] = heap[i];
        }
        heap = temp;
    }

    public static void main(String[] args) {
        MyPriorityQueue<Integer> pq = new MyPriorityQueue<>(3, Comparator.naturalOrder());
        pq.push(3);
        pq.push(1);
        pq.push(4);
        pq.push(1);
        pq.push(5);
        pq.push(9);
        // 1 1 3 4 5 9
        while (!pq.isEmpty()) {
            System.out.println(pq.pop());
        }
    }
}

go:

package main

import (
	"fmt"
	"errors"
)

type MyPriorityQueue struct {
	// 堆数组
	heap []interface{}

	// 堆中元素的数量
	size int

	// 元素比较器
	comparator func(x, y interface{}) int
}

// 构造函数
func NewMyPriorityQueue(capacity int, comparator func(x, y interface{}) int) *MyPriorityQueue {
	return &MyPriorityQueue{
		heap:       make([]interface{}, capacity),
		size:       0,
		comparator: comparator,
	}
}

// 返回堆的大小
func (pq *MyPriorityQueue) Size() int {
	return pq.size
}

// 判断堆是否为空
func (pq *MyPriorityQueue) IsEmpty() bool {
	return pq.size == 0
}

// 父节点的索引
func (pq *MyPriorityQueue) Parent(node int) int {
	return (node - 1) / 2
}

// 左子节点的索引
func (pq *MyPriorityQueue) Left(node int) int {
	return node*2 + 1
}

// 右子节点的索引
func (pq *MyPriorityQueue) Right(node int) int {
	return node*2 + 2
}

// 交换数组的两个元素
func (pq *MyPriorityQueue) Swap(i, j int) {
	pq.heap[i], pq.heap[j] = pq.heap[j], pq.heap[i]
}

// 查，返回堆顶元素，时间复杂度 O(1)
func (pq *MyPriorityQueue) Peek() (interface{}, error) {
	if pq.IsEmpty() {
		return nil, errors.New("priority queue underflow")
	}
	return pq.heap[0], nil
}

// 增，向堆中插入一个元素，时间复杂度 O(logN)
func (pq *MyPriorityQueue) Push(x interface{}) {
	// 扩容
	if pq.size == len(pq.heap) {
		pq.resize(2 * len(pq.heap))
	}
	// 把新元素追加到最后
	pq.heap[pq.size] = x
	// 然后上浮到正确位置
	pq.swim(pq.size)
	pq.size++
}

// 删，删除堆顶元素，时间复杂度 O(logN)
func (pq *MyPriorityQueue) Pop() (interface{}, error) {
	if pq.IsEmpty() {
		return nil, errors.New("priority queue underflow")
	}
	res := pq.heap[0]
	// 把堆底元素放到堆顶
	pq.Swap(0, pq.size-1)
	// 避免对象游离
	pq.heap[pq.size-1] = nil
	pq.size--
	// 然后下沉到正确位置
	pq.sink(0)
	// 缩容
	if pq.size > 0 && pq.size == len(pq.heap)/4 {
		pq.resize(len(pq.heap) / 2)
	}
	return res, nil
}

// 上浮操作，时间复杂度是树高 O(logN)
func (pq *MyPriorityQueue) swim(node int) {
	for node > 0 && pq.comparator(pq.heap[pq.Parent(node)], pq.heap[node]) > 0 {
		pq.Swap(pq.Parent(node), node)
		node = pq.Parent(node)
	}
}

// 下沉操作，时间复杂度是树高 O(logN)
func (pq *MyPriorityQueue) sink(node int) {
	for pq.Left(node) < pq.size {
		// 比较自己和左右子节点，看看谁最小
		minNode := node
		if pq.Left(node) < pq.size && pq.comparator(pq.heap[pq.Left(node)], pq.heap[minNode]) < 0 {
			minNode = pq.Left(node)
		}
		if pq.Right(node) < pq.size && pq.comparator(pq.heap[pq.Right(node)], pq.heap[minNode]) < 0 {
			minNode = pq.Right(node)
		}
		if minNode == node {
			break
		}
		// 如果左右子节点中有比自己小的，就交换
		pq.Swap(node, minNode)
		node = minNode
	}
}

// 调整堆的大小
func (pq *MyPriorityQueue) resize(capacity int) {
	newHeap := make([]interface{}, capacity)
	for i := 0; i < pq.size; i++ {
		newHeap[i] = pq.heap[i]
	}
	pq.heap = newHeap
}

func main() {
	pq := NewMyPriorityQueue(3, func(x, y interface{}) int {
		a := x.(int)
		b := y.(int)
		if a < b {
			return -1
		} else if a > b {
			return 1
		}
		return 0
	})

	pq.Push(3)
	pq.Push(1)
	pq.Push(4)
	pq.Push(1)
	pq.Push(5)
	pq.Push(9)

	// 1 1 3 4 5 9
	for !pq.IsEmpty() {
		item, _ := pq.Pop()
		fmt.Println(item)
	}
}