二叉搜索树的应用及可视化

一句话总结 二叉搜索树是特殊的二叉树结构，其主要的实际应用是 TreeMap 和 TreeSet。

前文几种常见的二叉树类型介绍二叉搜索树，接下来我会带你亲自实现一个类似 Java 标准库的 TreeMap 和 TreeSet 结构，帮助你知行合一。

不过呢，考虑到本文还处在数据结构基础的章节，本文仅讲解 TreeMap/TreeSet 的原理，动手实现 TreeMap/TreeSet 我放到了二叉树系列习题的后面。

因为和前面的哈希表、队列这些数据结构不同，树相关的数据结构需要比较强的递归思维，难度会上一个层级。如果你对递归的理解不够深入，现在给你讲的话不仅学习曲线有些陡峭，而且意义不大，就算你费了半天劲看懂了，遇到实际的题目还是不会，这很打击信心。

所以我建议循序渐进，后面二叉树的习题章节，用 100 多道实际的算法题手把手带你培养递归思维。刷完后你就可以秒杀所有二叉树相关的算法题了，再去看树相关的数据结构实现，就会感觉非常简单。甚至你都不用看我的代码，自己凭感觉就能实现 TreeMap/TreeSet。

好了，废话不多说，让我们开始吧。

二叉搜索树的优势

前文几种常见的二叉树类型介绍过二叉搜索树（BST）的特点，即左小右大：

对于树中的每个节点，其左子树的每个节点的值都要小于这个节点的值，右子树的每个节点的值都要大于这个节点的值。

比方说下面这棵树就是一棵 BST：

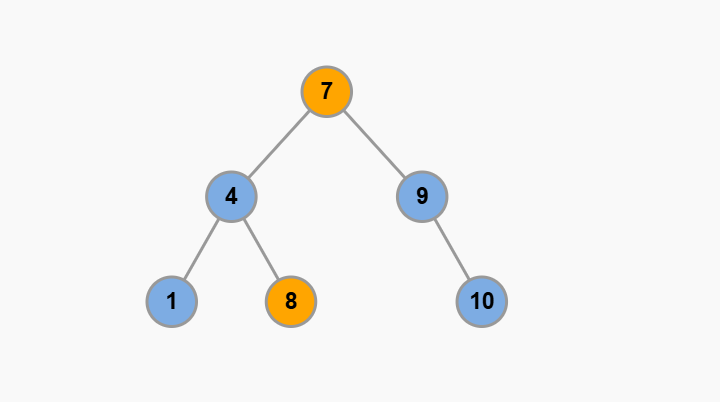
erchasousuoshu

这个左小右大的特性，可以让我们在 BST 中快速找到某个节点，或者找到某个范围内的所有节点，这是 BST 的优势所在。

你应该已经学过前文二叉树的遍历，下面用标准的二叉树遍历函数结合可视化面板来对比展示一下 BST 和普通二叉树的操作差别。

这里展示的是查找目标元素的场景，可以看到，利用 BST 左小右大的特性，可以迅速定位到目标节点，理想的时间复杂度是树的高度 O(logN)，而普通的二叉树遍历函数则需要 O(N) 的时间遍历所有节点。

至于其他增、删、改的操作，你首先查到目标节点，才能进行增删改的操作对吧？增删改的操作无非就是改一改指针，所以增删改的时间复杂度也是 O(logN)。

TreeMap/TreeSet 实现原理

你看 TreeMap 这个名字，应该就能看出来，它和前文介绍的哈希表 HashMap 的结构是类似的，都是存储键值对的，HashMap 底层把键值对存储在一个 table 数组里面，而 TreeMap 底层把键值对存储在一棵二叉搜索树的节点里面。

至于 TreeSet，它和 TreeMap 的关系正如哈希表 HashMap 和哈希集合 HashSet 的关系一样，说白了就是 TreeMap 的简单封装，所以下面主要讲解 TreeMap 的实现原理。

力扣经典的 TreeNode 结构长这样：

type TreeNode struct {
    Val   int
    Left  *TreeNode
    Right *TreeNode
}

我们只要改一改这个经典的 TreeNode 结构，就可以用来实现 TreeMap 了:

type TreeNode struct {
    Key   interface{}
    Value interface{}
    Left  *TreeNode
    Right *TreeNode
}

我们将实现的 TreeMap 结构有如下 API：

// TreeMap 主要接口
class MyTreeMap<K, V> {

    // ****** Map 键值映射的基本方法 ******

    // 增/改，复杂度 O(logN)
    public void put(K key, V value) {}

    // 查，复杂度 O(logN)
    public V get(K key) {}

    // 删，复杂度 O(logN)
    public void remove(K key) {}

    // 是否包含键 key，复杂度 O(logN)
    public boolean containsKey(K key) {}

    // 返回所有键的集合，结果有序，复杂度 O(N)
    public List<K> keys() {}

    // ****** TreeMap 提供的额外方法 ******

    // 查找最小键，复杂度 O(logN)
    public K firstKey() {}

    // 查找最大键，复杂度 O(logN)
    public K lastKey() {}

    // 查找小于等于 key 的最大键，复杂度 O(logN)
    public K floorKey(K key) {}

    // 查找大于等于 key 的最小键，复杂度 O(logN)
    public K ceilingKey(K key) {}

    // 查找排名为 k 的键，复杂度 O(logN)
    public K selectKey(int k) {}

    // 查找键 key 的排名，复杂度 O(logN)
    public int rank(K key) {}

    // 区间查找，复杂度 O(logN + M)，M 为区间大小
    public List<K> rangeKeys(K low, K high) {}
}

除了标准的增删查改方法 get, put, remove, containsKey 之外，TreeMap 还提供了很多额外方法，主要和 key 的大小相关。怎么样，是不是感觉很强大？

哈希表很实用，但是它确实没办法很好地处理键之间的大小关系。前文用链表加强哈希表中实现的 LinkedHashMap 也只是做到按「插入顺序」排列哈希表中的键，依然做不到按「大小顺序」排列。

下面简单介绍一下 TreeMap 的每个方法的实现原理，具体的代码在后文 TreeMap/TreeSet 的实现细说。

基本增删查改

首先，get 方法其实就类似上面可视化面板中查找目标节点的操作，根据目标 key 和当前节点的 key 比较，决定往左走还是往右走，可以一次性排除掉一半的节点，复杂度是 O(logN)。

至于 put, remove, containsKey 方法，其实也是要先利用 get 方法找到目标键所在的节点，然后做一些指针操作，复杂度都是 O(logN)。

floorKey, ceilingKey 方法是查找小于等于/大于等于某个键的最大/最小键，这个方法的实现和 get 方法类似，唯一的区别在于，当找不到目标 key 时，get 方法返回空指针，而 ceilingKey, floorKey 方法则返回和目标 key 最接近的键，类似上界和下界。

rangeKeys 方法输入一个 [low, hi] 区间，返回这个区间内的所有键。这个方法的实现也是利用 BST 的性质提高搜索效率：

如果当前节点的 key 小于 low，那么当前节点的整棵左子树都小于 low，根本不用搜索了；如果当前节点的 key 大于 hi，那么当前节点的整棵右子树都大于 hi，也不用搜索了。

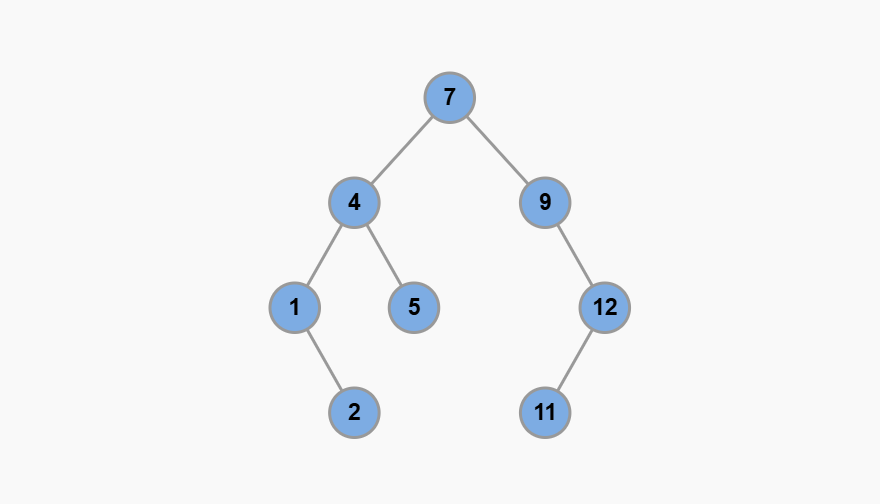
firstKey, lastKey 方法 firstKey 方法是查找最小键，lastKey 方法是查找最大键，借助 BST 左小右大的特性，非常容易实现：

从 BST 的根节点开始，一直往左走，最后遇到的非空节点就是最小的节点；同理，一直往右走，最后遇到的非空节点就是最大的节点。

你看看是不是这样，1 是最小的节点，12 是最大的节点：

erchashu3

keys 方法 keys 方法返回所有键，且结果有序。可以利用 BST 的中序遍历结果有序的特性。

selectKey, rank 方法 这两个方法比较有意思。其中 selectKey 方法是查找排名为 k 的键（从小到大，从 1 开始），rank 方法是查找目标 key 的排名。

比如下面这棵 BST，selectKey(3) 返回 5，因为元素 5 的大小排在第三；rank(10) 返回 6，因为元素 10 的排名是第六。

erchasousuoshu

keys [1, 4, 5, 7, 9, 10]
rank  1  2  3  4  5  6

先说 selectKey 方法，一个容易想到的方法是利用 BST 中序遍历结果有序的特性，中序遍历的过程中记录第 k 个遍历到节点，就是排名为 k 的节点。

但是这样的时间复杂度是 O(k)，因为你至少要用中序遍历经过 k 个节点。

一个更巧妙的办法是给二叉树节点中新增更多的字段记录额外信息：

class TreeNode<K, V> {
    K key;
    V value;
    // 记录以当前节点为根的子树的节点总数（包含当前节点）
    int size;

    TreeNode<K, V> left;
    TreeNode<K, V> right;

    TreeNode(K key, V value) {
        this.key = key;
        this.value = value;
        this.size = 1;
    }
}

erchasousuoshu

keys [1, 4, 5, 7, 9, 10]
rank  1  2  3  4  5  6
size  1  3  1  6  2  1

这样一来，selectKey 就可以利用这个 size 字段把时间复杂度降到 O(logN) 了。

因为 size 维护的就是当前节点为根的整棵树上有多少个节点，加上 BST 左小右大的特性，那么对于根节点，它只需要查询左子树的节点个数，就知道了自己在以自己为根的这棵树上的排名；知道了自己的排名，就可以确定目标排名的那个节点存在于左子树还是右子树上，从而避免搜索整棵树。

比方说上面的例子，你调用 selectKey(3) 找排名第三的节点，根节点 7 查看左子节点 4 得知左子树共有 3 个节点，加上自己共有 4 个节点，那么 7 就知道自己排名第四。

由此可知，排名第三的节点在 7 的左子树，就不用再往右子树找了。类似的，如果你调用 selectKey(5) 找排名第五的节点，7 就知道要往右子树找。

再说 rank 方法，也可以利用这个 size 字段。比方说你调用 rank(9)，想知道节点 9 这个元素排名第几，根节点 7 知道左子树有 3 个节点，加上自己共有 4 个节点，即自己排名第 4；然后 7 可以去右子树递归调用 rank(9)，计算节点 9 在右子树中的排名，最后再加上 4，就是整棵树中节点 9 的排名：

rank(node(7), 9) = 3 + 1 + rank(node(9), 9) = 3 + 1 + 1 = 5

当然，这样也提高了维护的复杂性，因为每次插入、删除节点都要动态地更新这个额外的 size 字段，确保它的正确性。

性能问题

前文说复杂度是树的高度 O(logN)（N 为节点总数），这是有前提的，即二叉搜索树要是「平衡」的，也就是左右子树的高度差不能太大，比如这样：

erchasousuoshu

可以直观地感觉到这棵树比较平衡，假设树中节点总数为 N，那么树的高度是 O(logN)。

如果搜索树不平衡，比如这种极端情况，所有节点都只有右子树，没有左子树：

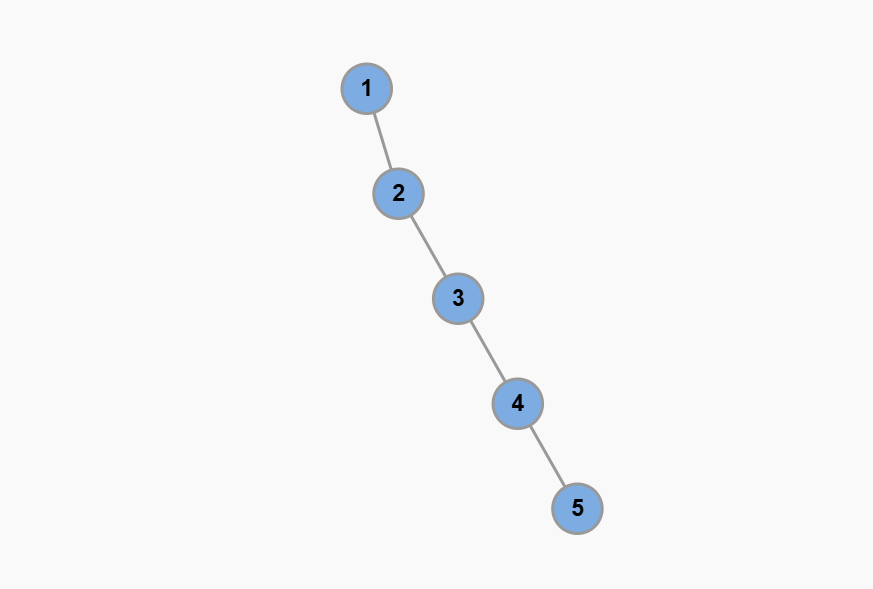
jiduanerchashu

这样二叉搜索树其实退化成了一条单链表，树的高度等于节点数 O(N)，这种情况下，即便这棵树符合 BST 的定义，但是性能就退化成了链表的性能，增删查改的复杂度全部变成了 O(N)。

可以这样说：二叉搜索树的性能取决于树的高度，树的高度取决于树的平衡性。因此，在实际应用中，TreeMap 需要自动维护树的平衡，避免出现性能退化。

如何自动维护平衡性？这可就复杂了。你需要在插入和删除二叉树节点的时候对树进行局部旋转操作，比方上面那棵退化成单链表的 BST，可以这样被旋转成平衡二叉树：

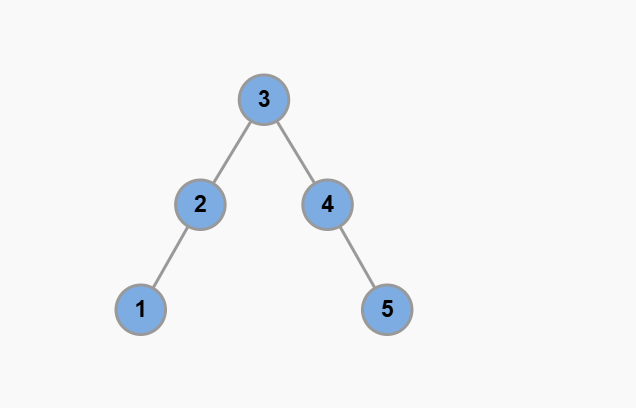
erchashu4

大家熟知的红黑树就是一类自平衡的二叉搜索树，它的平衡性能非常好，但是实现起来比较复杂，这就是完美所需付出的代价。

目前我们实现的 TreeMap 仅使用普通 BST 而不是实现红黑树。红黑树的实现目前还没有更新到网站

好了，本文就介绍这么多，上面只说了每个方法的实现思路，具体的代码实现在后文 TreeMap/TreeSet 的实现细说，建议你循序渐进，按照本站目录顺序先完成二叉树系列习题，再去学习 TreeMap 的代码。