用链表加强哈希表(LinkedHashMap)
前文 哈希表原理 从原理上分析了,不能依赖哈希表遍历 key 的顺序,即哈希表中的 key 是无序的。
但结合实际的编程经验,你可能会有些疑问。
比如熟悉 Python 的读者可能知道,Python 3.7 开始,标准库提供的哈希表 dict 就明确告诉你了,dict 的键的遍历顺序就是键的插入顺序。比如下面这段简单的代码:
d = dict()
d['a'] = 1
d['b'] = 2
d['c'] = 3
print(list(d.keys())) # ['a', 'b', 'c']
d['y'] = 4
print(list(d.keys())) # ['a', 'b', 'c', 'y']
d['d'] = 5
print(list(d.keys())) # ['a', 'b', 'c', 'y', 'd']
无论你插入多少键,keys 方法返回的所有键都是按照插入顺序排列,感觉就好像在向数组尾部追加元素一样。这怎么可能呢?
如果你熟悉 Golang,你会发现一个更神奇的现象。比如下面这段测试代码:
package main
import (
"fmt"
)
func main() {
// 初始化 map
myMap := map[string]int{
"1": 1,
"2": 2,
"3": 3,
"4": 4,
"5": 5,
}
// 定义遍历 map 的函数
printMapKeys := func(m map[string]int) {
for key := range m {
fmt.Print(key, " ")
}
fmt.Println()
}
// 多次遍历 map,观察键的顺序
printMapKeys(myMap)
printMapKeys(myMap)
printMapKeys(myMap)
printMapKeys(myMap)
}
// 我运行的结果如下:
// 1 2 3 4 5
// 5 1 2 3 4
// 2 3 4 5 1
// 1 2 3 4 5
也就是说,它每次遍历的顺序都是随机。但是按照前文 哈希表原理 所说,虽然哈希表的键是无序的,但是没有对哈希表做任何操作,遍历得到的结果应该不会变才对,Golang 的 map 每次遍历的顺序咋都不一样?这也太离谱了吧?
你可以先自己思考下原因,下面我给出答案。
**先说 Golang 吧,每次遍历都乱序的原因就是,它故意的**。
这个原因属实是让人有些哭笑不得,Golang 为了防止开发者依赖哈希表的遍历顺序,所以每次遍历都故意返回不同的顺序,可谓用心良苦。也可以从侧面看出,确实不少开发者没了解过哈希表的基本原理。
我们不妨进一步想想,它是怎么打乱顺序的呢?真是随机打乱吗?
其实不是,你仔细看看,它这个乱序是有规律的。有没有想起前面讲过的[环形数组](05-环形数组技巧及实现.md)?
```text
| 1 2 3 4 5
5 | 1 2 3 4
2 3 4 5 | 1
| 1 2 3 4 5
```
看出来没有?如果不触发扩缩容的话,实际上它的遍历顺序应该也是固定的,只不过它不是每次都从底层 table 数组的头部开始,而是从一个随机的位置开始,然后利用环形数组技巧遍历整个 table 数组,这样就能保证多次遍历的结果具有随机性,同时又不至于为了随机性而牺牲太多性能。
再说 **Python,它能让所有键按照插入顺序排列,是因为它把标准的哈希表和链表结合起来,组成了一种新的数据结构:哈希链表**。
其他编程语言也有类似的实现,比如 Java 的 LinkedHashMap。这种数据结构兼具了哈希表 O(1) 的增删查改效率,同时又可以像数组链表一样保持键的插入顺序。
它是怎么做的呢?下面我会具体讲解。
哈希链表(LinkedHashMap)实现思路
我们先明确一下问题。
标准哈希表的键是无序存储在底层的 table 数组中的:
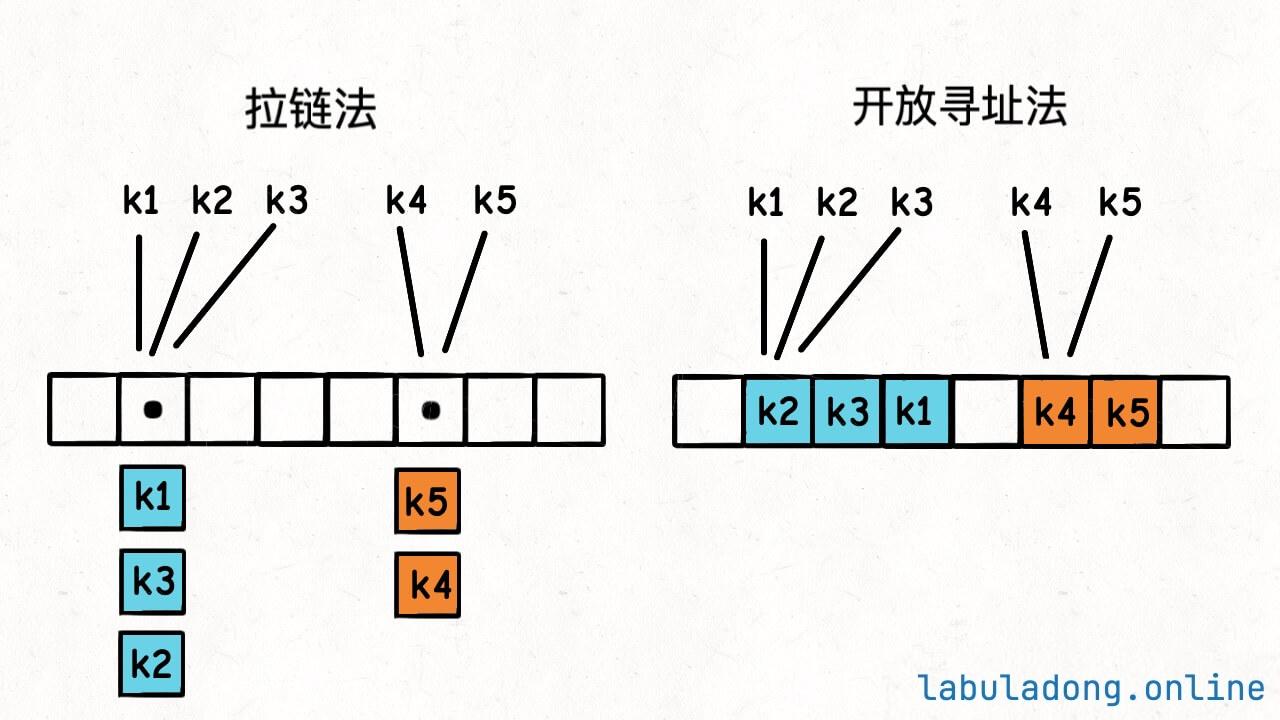
你光看这个图,看不出来这些键是按什么顺序插入的,且一旦触发扩缩容,这键的位置又会改变。
我们现在希望在不改变哈希表增删查改复杂度的前提下,能够按照插入顺序来访问所有键,且不受扩缩容影响。
那么一个最直接的思路就是,我想办法把这些键值对都用类似链表节点的结构串联起来,持有一个头尾结点 head, tail 的引用,每次把新的键插入 table 数组时,同时把这个键插入链表的尾部。
这样一来,只要我从头结点 head 开始遍历链表,就能按照插入顺序访问所有键了:
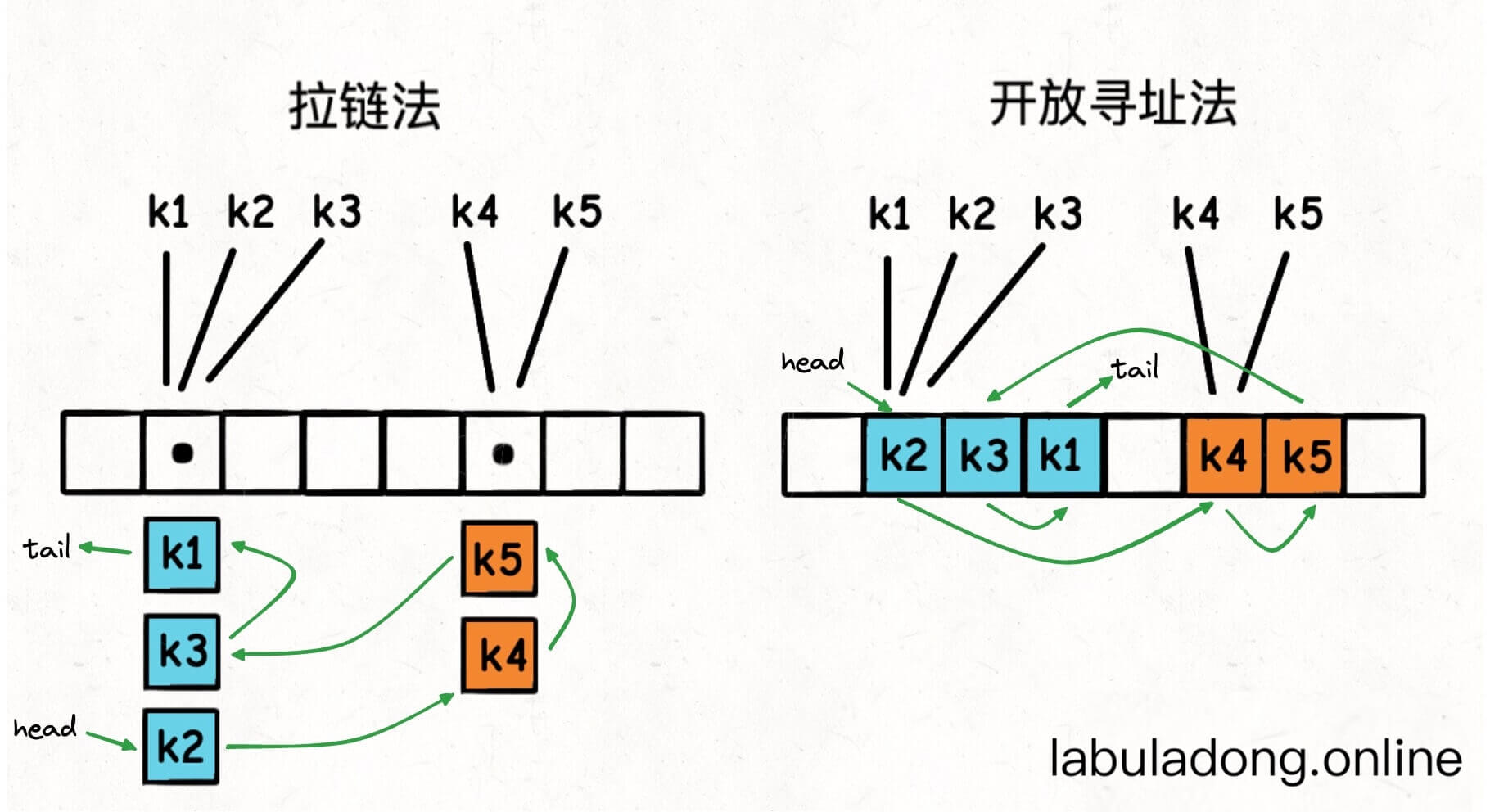
我们可以清楚地看出,键的插入顺序是 k2, k4, k5, k3, k1。
**发挥抽象思维,不要陷入细节**
但肯定有读者会绕晕:之前[拉链法实现哈希表](12-用拉链法实现哈希表.md) 不就是用链表解决哈希冲突的吗?现在相当于在链表上再套一层链表?这咋实现啊?
所以我在本站的开篇就说,要有抽象能力。你看所有数据结构,本质上就是在数组、链表这两种基本结构上雕花,但即便如此,多套几层你也晕了。
如果产生这样的疑问,是因为你脑子里全是前两章讲的拉链法、线性探查法的底层实现原理,陷入细节无法自拔了,是不是这样?
请跳出细节,抽象来看,哈希表本质上就是一个键值映射,链表本质上就是一个顺序存储元素的容器。现在我就是想让这个键值映射中的键按照插入顺序排列,怎么把哈希表和链表结合起来?
答案是这样:
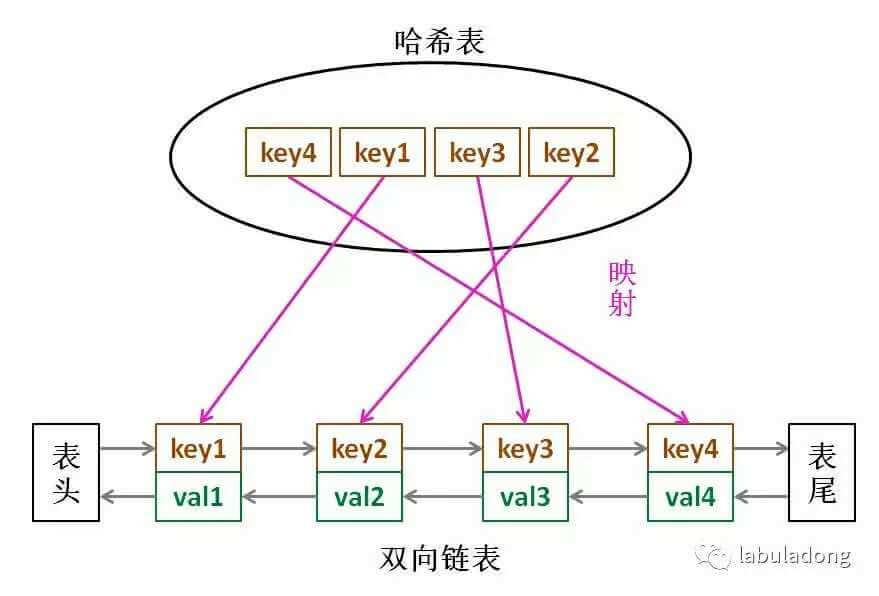
假设键和值都是字符串类型,标准的哈希表是这样:
HashMap<String, String> map = new HashMap<>();
// 插入键值对
String key = "k1";
String value = "v1";
map.put(key, value);
而我们现在给哈希表的值类型套了一层双链表结构:
// 双链表节点
class Node {
String key;
String value;
Node prev;
Node next;
Node(String key, String value) {
this.key = key;
this.value = value;
}
}
HashMap<String, Node> map = new HashMap<>();
// 插入键值对
String key = "k1";
String value = "v1";
map.put(key, new Node(key, value));
// 这里做了简化,实际实现中还要操作新的链表节点加入链表
这样一来,就实现了哈希链表结构:
- 我们还是可以在 O(1) 的时间复杂度内通过键查找到对应的双链表节点,进而找到键对应的值。
- 我们可以在 O(1) 的时间复杂度内插入新的键值对。因为哈希表本身的插入操作时间复杂度是 O(1),且双链表头尾的插入操作时间复杂度也是 O(1)。
- 我们可以在 O(1) 的时间复杂度内删除指定的键值对。因为哈希表本身的删除操作时间复杂度是 O(1),删除给定双链表节点的操作时间复杂度也是 O(1)。
- 由于链表节点的顺序是插入顺序,那么只要从头结点开始遍历这个链表,就能按照插入顺序访问所有键。
也就是说,我们在不改变标准哈希表的基本操作复杂度的前提下,实现了按照插入顺序访问所有键的需求。
链表的删除操作时间复杂度是 O(1)?
肯定有读者记得,前文
链表原理 说过,链表的删除操作时间复杂度是 (n) 啊,怎么现在又说是 O(1) 了?
实际上我说的已经很严谨了,我这里说的是 **删除给定双链表节点的操作是 O(1)**。
前文我们动手实现链表的时候,我们是删除指定索引的链表节点,时间复杂度确实是 O(n),因为要先遍历到这个索引,然后才能开始删除嘛。
但是这里并没有遍历的过程,我们是直接通过哈希表键值映射拿到的这个链表节点,时间复杂度是 O(1)。
且双链表节点只需进行简单的指针操作即可把自身从链表中删除,时间复杂度是 O(1):
```java
// 删除给定双链表节点
Node target;
// 在双链表中删除 target 节点
target.prev.next = target.next;
target.next.prev = target.prev;
target.prev = null;
target.next = null;
```
所以哈希链表删除操作的复杂度依然是 O(1)。
这里需要注意,双链表节点同时拥有前后驱指针,才可以做到 O(1) 时间复杂度的删除操作。单链表节点只有后驱指针,但没有前驱指针,做不到 O(1) 时间复杂度的删除操作。所以哈希链表的实现中,只能使用双链表。
代码实现
明白了哈希链表的原理,直接看代码实现吧,比较简单:
package main
import "fmt"
type MyLinkedHashMap struct {
head *Node
tail *Node
m map[string]*Node
}
type Node struct {
key string
val int
next *Node
prev *Node
}
func Constructor() MyLinkedHashMap {
head := &Node{}
tail := &Node{}
head.next = tail
tail.prev = head
return MyLinkedHashMap{
head: head,
tail: tail,
m: make(map[string]*Node),
}
}
func (this *MyLinkedHashMap) Get(key string) int {
if node, ok := this.m[key]; ok {
return node.val
}
return -1
}
func (this *MyLinkedHashMap) Put(key string, val int) {
// 若为新插入的节点,则同时插入链表和 map
if _, ok := this.m[key]; !ok {
// 插入新的 Node
node := &Node{key: key, val: val}
this.addLastNode(node)
this.m[key] = node
return
}
// 若存在,则替换之前的 val
this.m[key].val = val
}
func (this *MyLinkedHashMap) Remove(key string) {
// 若 key 本不存在,直接返回
if _, ok := this.m[key]; !ok {
return
}
// 若 key 存在,则需要同时在哈希表和链表中删除
node := this.m[key]
delete(this.m, key)
this.removeNode(node)
}
func (this *MyLinkedHashMap) ContainsKey(key string) bool {
_, ok := this.m[key]
return ok
}
func (this *MyLinkedHashMap) Keys() []string {
keyList := make([]string, 0)
for p := this.head.next; p != this.tail; p = p.next {
keyList = append(keyList, p.key)
}
return keyList
}
func (this *MyLinkedHashMap) addLastNode(x *Node) {
temp := this.tail.prev
// temp <-> tail
x.next = this.tail
x.prev = temp
// temp <- x -> tail
temp.next = x
this.tail.prev = x
// temp <-> x <-> tail
}
func (this *MyLinkedHashMap) removeNode(x *Node) {
prev := x.prev
next := x.next
// prev <-> x <-> next
prev.next = next
next.prev = prev
x.next = nil
x.prev = nil
}
func main() {
myMap := Constructor()
myMap.Put("a", 1)
myMap.Put("b", 2)
myMap.Put("c", 3)
myMap.Put("d", 4)
myMap.Put("e", 5)
// output: a b c d e
fmt.Println(myMap.Keys())
myMap.Remove("c")
// output: a b d e
fmt.Println(myMap.Keys())
}
LinkedHashSet 的实现
LinkedHashSet 就是一个可以保持插入顺序的哈希集合。
前文 哈希集合的原理及实现 说过,哈希集合的代码实现其实就是包装了一下哈希表。
所以这里 LinkedHashSet 的实现也是直接包装一下 MyLinkedHashMap 即可,非常简单,我就不写代码了。