对列和栈基本原理

计算机的两种存储方式，顺序存储（数组）和链式存储（链表）都讲完了，之后的所有数据结构都是基于这两种存储方式之上玩花活。

本文讲解队列和栈的基本原理，后面的文章会讲解如何用代码具体实现。

先说概念吧，其实队列和栈都是「操作受限」的数据结构。说它操作受限，主要是和基本的数组和链表相比，它们提供的 API 是不完整的。

比方说我们前面实现的数组和链表，增删查改的 API 都实现过了，你可以对任意一个索引元素进行增删查改，只要索引不越界，就随便你。

但是对于队列和栈，它们的操作是受限的：队列只能在一端插入元素，另一端删除元素；栈只能在某一端插入和删除元素。说白了就是把数组链表提供的 API 删掉了一部分，只保留头尾操作元素的 API 给你用。

形象地理解，队列只允许在队尾插入元素，在队头删除元素，栈只允许在栈顶插入元素，从栈顶删除元素。这个图中把栈竖着画，队列横着画，只是为了更形象，但实际上它们底层都是数组和链表实现的，后面会讲到：

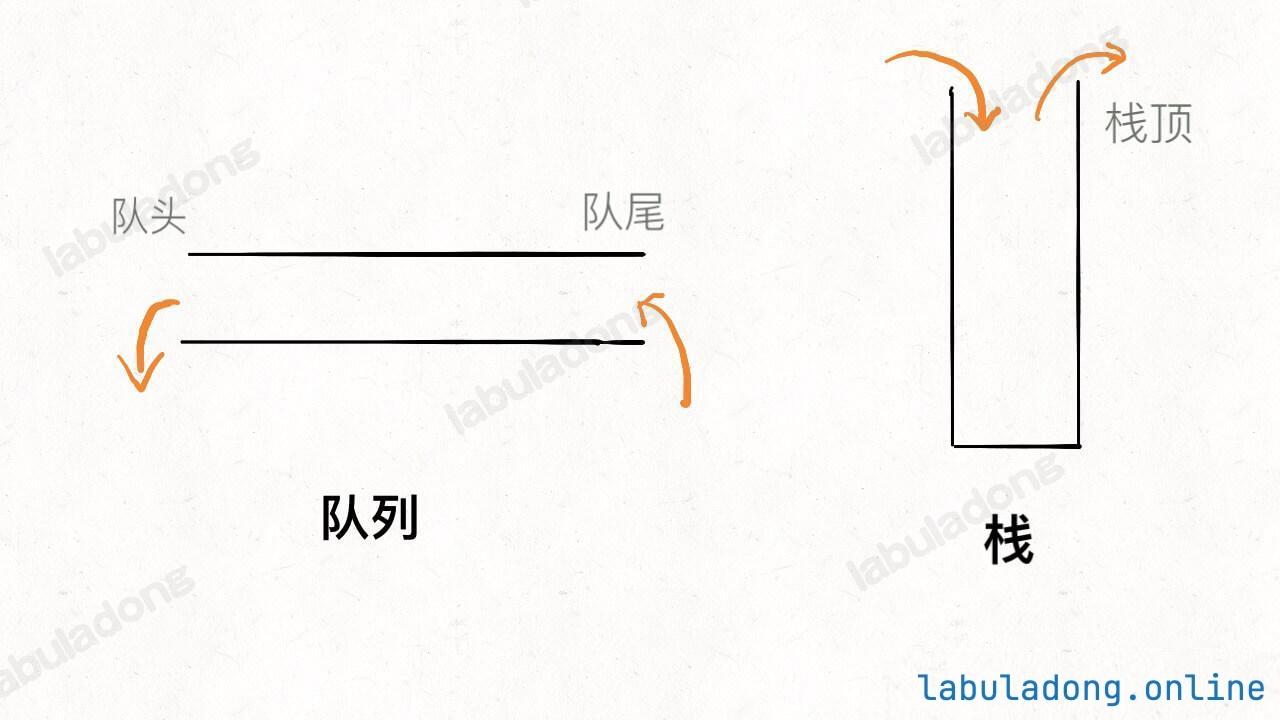
队列就像排队买票，先来的先离开，后来的后离开；栈就像一摞盘子，最先放的压在最下面，最后放的留在最上面，拿的时候也是最上面的先被拿走。所以我们常说，队列是一种「先进先出」的数据结构，栈是一种「先进后出」的数据结构，就是这个道理。

这两种数据结构的基本 API 如下：

// 队列的基本 API
type MyQueue[T any] struct {
}

// 向队尾插入元素，时间复杂度 O(1)
func (q *MyQueue[T]) Push(e T) {}

// 从队头删除元素，时间复杂度 O(1)
func (q *MyQueue[T]) Pop() T {}

// 查看队头元素，时间复杂度 O(1)
func (q *MyQueue[T]) Peek() T {}

// 返回队列中的元素个数，时间复杂度 O(1)
func (q *MyQueue[T]) Size() int {}

// 栈的基本 API
type MyStack[T any] struct {
}

// 向栈顶插入元素，时间复杂度 O(1)
func (s *MyStack[T]) Push(e T) {}

// 从栈顶删除元素，时间复杂度 O(1)
func (s *MyStack[T]) Pop() T {}

// 查看栈顶元素，时间复杂度 O(1)
func (s *MyStack[T]) Peek() T {}

// 返回栈中的元素个数，时间复杂度 O(1)
func (s *MyStack[T]) Size() int {}

不同编程语言中，队列和栈提供的方法名称可能不一样，但每个方法的效果肯定是一样的。

有些语言的标准库可能没有直接提供队列和栈，你可以自己用数组或者链表模拟出队列和栈的效果。下一章我就会先带你用链表实现队列和栈。