妙用二叉树后序位置:归并排序
一句话总结
归并排序的核心思路需要结合 二叉树的后序遍历 来理解:先利用递归把左右两半子数组排好序,然后在二叉树的后序位置合并两个有序数组。
考虑到这里是基础知识章节,我只会讲一下归并排序的整体思路,具体的代码实现和算法运用会安排在二叉树章节后面的 归并排序详解及运用 里,不建议初学者现在去看。
因为归并排序算法需要熟练掌握递归思维,且需要用到 双指针技巧 来合并两个有序数组,所以建议初学者按照本站目录顺序学习,到时候理解归并排序的代码会比较轻松。
归并排序核心思路
开头的这句总结虽然也比较抽象,但是有上一章 快速排序核心思路 的铺垫,你应该有点感觉。我用快速排序的思路来对比一下,你就能直观感受到它俩的区别了:
前文快速排序的思路是,先把一个元素放到正确的位置(排好序),然后将这个元素左右两边剩下的元素利用递归分别排好序,最终整个数组就排好序了。代码框架如下:
func sort(nums []int, lo int, hi int) {
if lo >= hi {
return
}
// ****** 前序位置 ******
// 对 nums[lo..hi] 进行切分,将 nums[p] 排好序
// 使得 nums[lo..p-1] <= nums[p] < nums[p+1..hi]
p := partition(nums, lo, hi)
// 去左右子数组进行切分
sort(nums, lo, p-1)
sort(nums, p+1, hi)
}
本文归并排序的思路是,把数组切成两半,先把这两半子数组分别排好序,然后再合并这两个有序数组,整个数组就排好序了。
// 定义:排序 nums[lo..hi]
func sort(nums []int, lo, hi int) {
if lo == hi {
return
}
mid := (lo + hi) / 2
// 利用定义,排序 nums[lo..mid]
sort(nums, lo, mid)
// 利用定义,排序 nums[mid+1..hi]
sort(nums, mid+1, hi)
// ****** 后序位置 ******
// 此时两部分子数组已经被排好序
// 合并两个有序数组,使 nums[lo..hi] 有序
merge(nums, lo, mid, hi)
}
本来我们的目标就是要排序数组的,你现在不告诉我具体怎么操作排序,反而让我去先把左右两半子数组先排好序,这不是等于没说么?我咋知道怎么去排序左右子数组呢?
这就是计算机思维中很有趣的一点:
你不要盯着整个问题,而是要向内求,去分解,分解,再分解,分无可分的那个基本单元,才是解决问题的关键。
只要把把那个最基本的单元研究清楚了,原问题,乃至百千万亿规模的问题,都将迎刃而解。
具体来说,让你排序 1 万个元素,你不要像基本排序算法那样上来就埋头干活,而是要来一波一尺之捶,日取其半的操作:
```text
10000 / 2 = 5000
5000 / 2 = 2500
2500 / 2 = 1250
1250 / 2 = 625
625 / 2 = 312
...
9 / 2 = 4
4 / 2 = 2
2 / 2 = 1
```
当分无可分的时候,答案就出来了,只剩一个元素的时候,还需要什么排序操作吗?它自己就是有序的,对吧?
好了,那么左右两半数组被分解成 1 个元素,已经排好序了。接下来 `merge` 函数上场,其实就是两个元素比较交换一下就能合并成一个长度为 2 的有序数组,对吧?
你现在都能 1 生 2 了,能不能 2 生 4,4 生 8,乃至生万物?最终,整个数组的所有元素都会被排序。
果然智慧都是相通的,让老子庄子醒过来,他们妥妥的计算机科学家。
排序稳定性
归并排序的稳定性取决于 merge 函数的实现,需要用到 双指针技巧。现在你可以先记住,归并排序是稳定排序。
时间复杂度
归并排序算法的 merge 函数也要遍历输入的数组 nums[lo..hi],和前文快速排序的 partition 函数一样,所以时间复杂度的计算法方法和快速排序类似,也是要看二叉树上的数组元素总数:
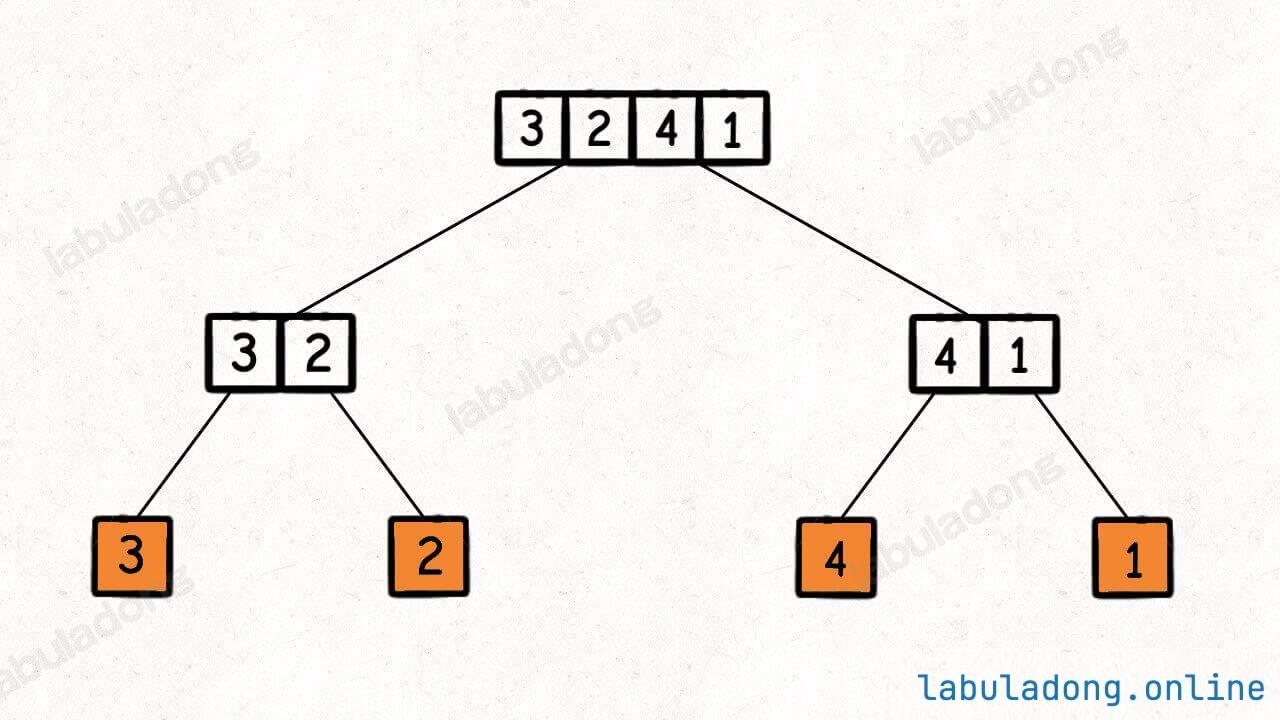
每向下一层,每个节点的数组元素就减半,但是每一层总的元素数量就是数组的长度 O(n)。
这棵二叉树是平衡二叉树,即树高是 O(logn),所以总的时间复杂度是 O(nlogn),即树高乘以每层的复杂度。
是否是原地排序?
不是原地排序。归并排序的 merge 函数需要一个额外的数组来辅助进行有序数组的合并操作,消耗 O(n) 的空间。