妙用二叉树前序位置：快速排序

一句话总结

快速排序的核心思路需要结合二叉树的前序遍历来理解：在二叉树遍历的前序位置将一个元素排好位置，然后递归地将剩下的元素排好位置。

正常人要排序数组，一般就是维护一个 sortedIndex，保持 [0, sortedIndex) 有序，逐步右移 sortedIndex，直到整个数组有序。这中间历经种种坎坷，逢山开路遇水搭桥，正如我们前面讲的选择排序、冒泡排序、插入排序、希尔排序。

但是越是效率高的算法，离计算机思维越近，未经训练的人就越难理解。学过前面几种基础排序算法，现在你应该可以感觉到这一点了，容易理解和推导的排序算法复杂度全都是 O(n²)，而突破 O(n²) 的排序算法，都感觉不是人类能想出来的。

哪个人要是张嘴就说：排序数组简单啊，只要把一个元素排好序，然后把剩下元素排好序，就能把整个数组排好序了。那只能说这个人可能是三体人潜伏在地球的特务：）

所幸我们可以站在前人的肩膀上理解这些奇思妙想，培养自己的计算机思维，这就是学习算法的目的。

回到正题，我们来讲一下快速排序。考虑到这里是基础知识章节，我只会讲一下快速排序的整体思路，具体的代码实现和算法运用会安排在二叉树章节后面的快速排序详解及运用里，不建议初学者现在去看，按照本站目录顺序，刷完二叉树章节的习题再去理解代码会比较轻松。

快速排序核心思路

快速排序的基本思路是这样的：

1、在 nums 数组中任意选择一个元素作为切分元素 pivot（一般选择第一个元素）。

 [4, 1, 7, 2, 8, 5, 3, 6, 9]
  ^
pivot

2、对数组中的元素进行若干交换操作，将小于 pivot 的元素放到 pivot 的左边，大于 pivot 的元素放到 pivot 的右边（换句话说，其实就是将 pivot 这一个元素排好序）。

 [3, 1, 2, 4, 8, 5, 7, 6, 9]
           ^
         pivot

3、递归地对 pivot 左边的数组和右边的数组重复上述步骤：寻找新的切分元素，然后交换元素，使得切分元素左侧都元素都比它小，右侧都元素都比它大（换句话说，其实就是递归的去把 pivot 左右两侧的其他元素排好序）。

 [3, 1, 2] [4] [8, 5, 7, 6, 9]
  ^         ^   ^
pivot1          pivot2

 [1, 2, 3] [4] [5, 7, 6, 8, 9]
        ^   ^            ^
    pivot1             pivot2

4、递归地重复上述操作，直到所有元素都放到正确的位置：

 [1] [2] [3] [4] [5] [6] [7] [8] [9]

所以我说快速排序的思路是：先把一个元素排好序，然后去把剩下的元素排好序。

代码框架

根据上述思路描述，可以写出快速排序的代码框架，代码中的 nums[p] 就是上面所说的 pivot 元素：

func sort(nums []int, lo int, hi int) {
    if lo >= hi {
        return
    }
    // ****** 前序位置 ******
    // 对 nums[lo..hi] 进行切分，将 nums[p] 排好序
    // 使得 nums[lo..p-1] <= nums[p] < nums[p+1..hi]
    p := partition(nums, lo, hi)

    // 去左右子数组进行切分
    sort(nums, lo, p-1)
    sort(nums, p+1, hi)
}

其中 partition 函数的实现是快速排序的核心，即遍历 nums[lo..hi]，将切分点元素 pivot 放到正确的位置，并返回该位置的索引 p。

如果你还有印象的话，这个代码框架就是二叉树遍历基础里的前序遍历框架，所以我说快速排序的本质是二叉树的前序遍历，在前序位置将 nums[p] 排好序，然后递归排序左右元素：

// 二叉树的遍历框架
func traverse(root *TreeNode) {
    if root == nil {
        return
    }
    // 前序位置
    traverse(root.Left)
    // 中序位置
    traverse(root.Right)
    // 后序位置
}

Important

快速排序代码框架中的 sort 函数功能等同于二叉树的遍历框架中的 traverse 函数，用来遍历所有节点（数组元素），对每个节点（数组元素）调用 partition 函数，将该节点（数组元素）放到正确的位置。

遍历完成后，所有数组元素都放到了正确的位置，整个数组就排好序了。

至于 partition 函数的思路，在你学习完 链表双指针技巧汇总 和 数组双指针技巧汇总 后就容易理解了。

时间复杂度

把快速排序抽象成一棵二叉树，每个二叉树节点都要遍历一遍数组（执行 partition 函数），总的时间复杂度是下面这棵树中数组元素的总数：

       [4, 1, 7, 2, 5, 3, 6]
         /                 \
    [2, 1, 3]    [4]     [7, 5, 6]
     /     \              /     \
  [1]  [2]  [3]        [5]  [6]  [7]

虽然节点每向下生长一层，每个二叉树节点对应的数组长度就减半，但是我们可以一整层一整层的看，每一层的数组元素总数都大致是数组长度 O(n)。

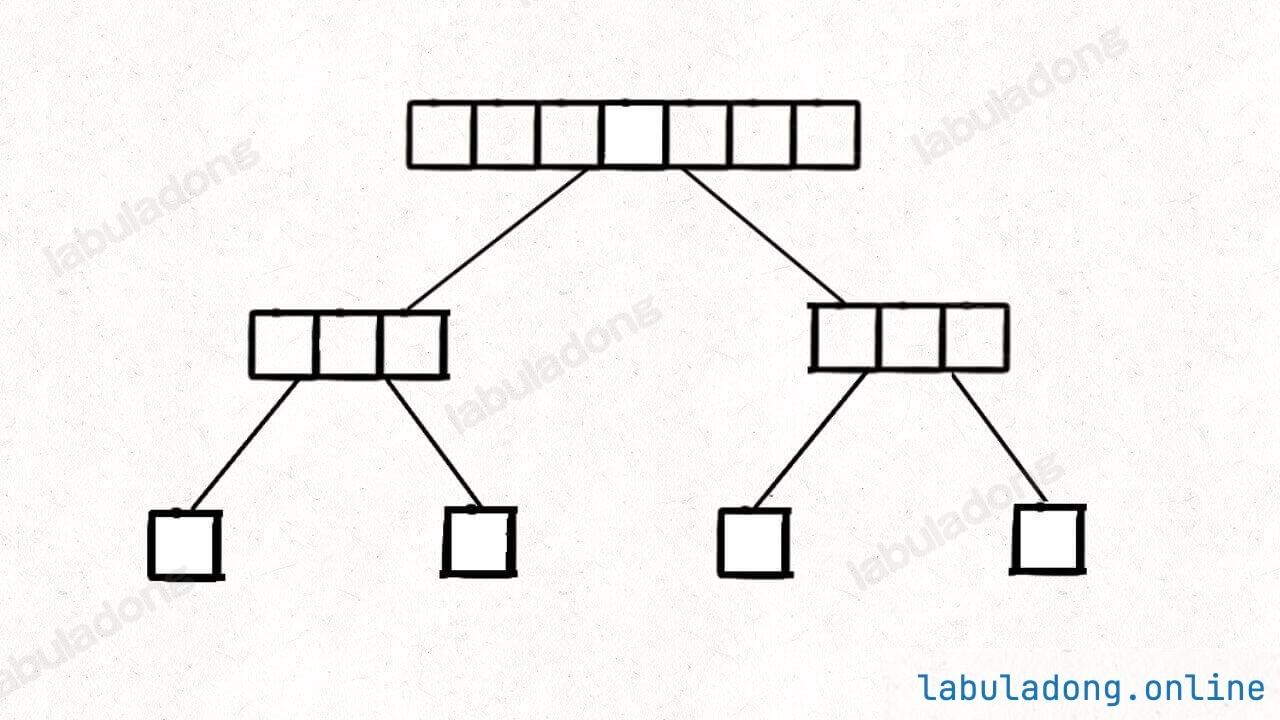
erchakuaisupaixu

理想情况这棵树是平衡二叉树，即树高是 O(logn)，所以总的时间复杂度是 O(nlogn)，即树高乘以每层的复杂度。

当然，上述分析是理想情况，快速排序遇到某些极端情况，复杂度会退化，具体可以参见快速排序详解及运用，这里就不展开了。

空间复杂度

快速排序不需要额外的辅助空间，是原地排序算法。

递归遍历二叉树时，递归函数的堆栈深度为树的高度，所以空间复杂度是 O(logn)。

稳定性

快速排序是不稳定排序算法，因为在 partition 函数中，不会考虑相同元素的相对位置，所以相同元素的相对位置可能会发生变化。

好了，对于快速排序的基本思路、时间复杂度、空间复杂度和稳定性，我就讲到这里，更详细的代码实现和算法运用安排在二叉树章节后面的快速排序详解及运用，建议你按照本站章节的顺序循序渐进地学习。